|
De sinusregel
In elke driehoek $ABC$ geldt de sinusregel:
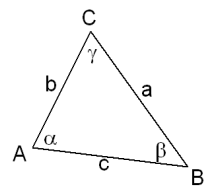
$\eqalign{\frac{a}{\sin(\alpha)}=\frac{b}{\sin(\beta)}=\frac{c}{\sin(\gamma)}}$
Voorbeeld
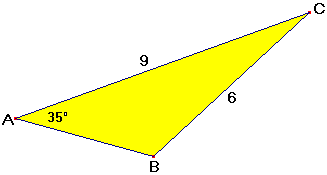
-
Bereken $\angle B$ in hele graden nauwkeurig.
Uitwerking
$\eqalign{\frac{6}{{\sin 35^\circ }} = \frac{9}{{\sin \beta }}}$
$6 \cdot \sin \beta = 9 \cdot \sin 35^\circ$
$\eqalign{\sin \beta = \frac{{9 \cdot \sin 35^\circ }}{6} \approx 0,860}$
$\beta \approx 59^\circ \,\,of\,\,\beta \approx 121^\circ$
Als de tekening zo'n beetje klopt dan moet $\angle B\approx 121^\circ$ zijn. |
De sinusregel in stomphoekige driehoeken
In het voorbeeld op deze pagina kan je zien dat er bij een gegeven waarde voor de sinus twee hoeken mogelijk zijn, een scherpe en een stompe hoek.
-
$\sin (\alpha ) = 0,722 \Rightarrow \alpha\approx 46^\circ\vee\alpha\approx 134^\circ$
Tot nu toe ben je de sinus alleen tegen gekomen in rechthoekige driehoeken. Je hebt dan geen stompe hoeken, maar er bestaat een waarde voor de sinus voor alle hoeken...
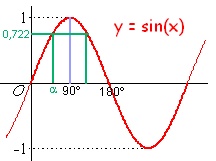
In bovenstaande grafiek kun je zien waarom je bij de sinus twee antwoorden kan krijgen.
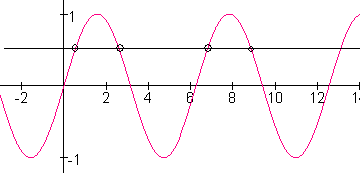
Eigenlijk is het nog veel erger... Er zijn oneindig veel hoeken met dezelfde waarde voor de sinus...
|










