|
Asymptoten
In een gebroken functie komt de variabele in de noemer van een breuk voor.
De eenvoudigste gebroken functie is $\eqalign{f(x)=\frac{1}{x}}$. De functie is een standaardfunctie. De grafiek van deze functie is een standaardgrafiek en heet hyperbool.
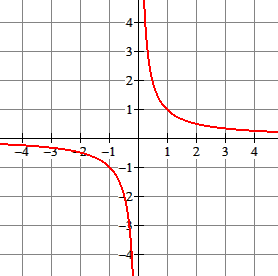
De grafiek bestaat uit twee losse delen. Deze heten de takken van de hyperbool.
Asymptoten
Als je bij $\eqalign{f(x)=\frac{1}{x}}$ voor $x$ een steeds groter getal neemt dan wordt de functiewaarde steeds kleiner. De functiewaarde komt steeds dichter bij y=0 te liggen.
De $x$-as (de lijn y=0) is de horizontale asymptoot van de grafiek van $f$.
Als je voor $x$ getallen neemt die steeds dichter bij 0 liggen dan wordt de functiewaarde steeds groter (of kleiner van de andere kant).
De $y$-as (de lijn x=0) is de verticale asymptoot van de grafiek van $f$.
-
Een asymptoot is een lijn waarmee de grafiek op den duur vrijwel samenvalt.
Zie over het vinden van asymptoten
|
Gebroken vergelijkingen
De vergelijking $\eqalign{\frac{x+2}{x+1}=\frac{6}{x+3}}$ is een gebroken vergelijking.
Je kunt de vergelijking algebraisch oplossen door kruislings vermenigvuldigen.
Het is verstandig om achteraf de gevonden oplossingen te controleren. Het is daarbij voldoende om na te gaan of voor de gevonden waarden van $x$ geen noemer nul wordt.
Voorbeeld
$
\eqalign{
& {{x + 2} \over {x + 1}} = {6 \over {x + 3}} \cr
& \left( {x + 2} \right)(x + 3) = 6(x + 1) \cr
& x^2 + 5x + 6 = 6x + 6 \cr
& x^2 - x = 0 \cr
& x(x - 1) = 0 \cr
& x = 0 \vee x = 1 \cr}
$
Beide oplossingen voldoen.
Regels voor het algebraisch oplossen van gebroken vergelijkingen
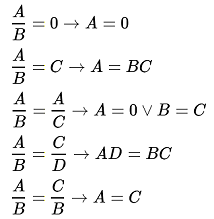
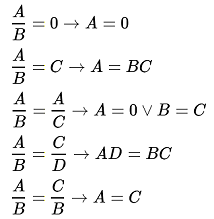
Zie voorbeelden gebroken vergelijkingen
 gebroken vergelijkingen
|
