|
Een formule van een sinusoide opstellen
Bij een sinusoide moet je een formule kunnen opstellen.

|
Uitwerking opdracht 1
Kijk eerst naar het hoogste en laagste punt. Je weet dan de evenwichtsstand en de amplitude:
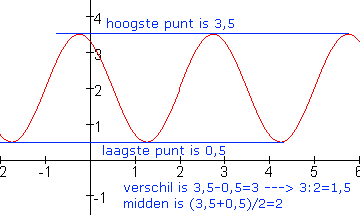
We zien: a=2 en b=1,5
|
|
Opdracht 1
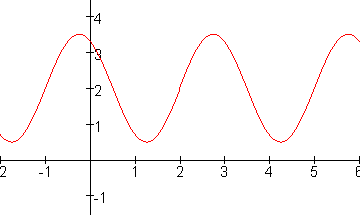
|
Uitwerking opdracht 1 vervolg
Kijk dan naar de periode en t0:
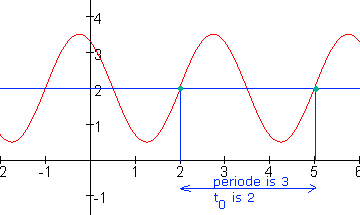
We zien T=3, dus c=$\frac{2\pi}{3}$ en t0=2. De formule wordt:
-
$h(t) = 2 + 1,5 \cdot \sin \left( {\frac{{2\pi }}{3}\left( {t - 2} \right)} \right)$
|
|
Opdracht 2
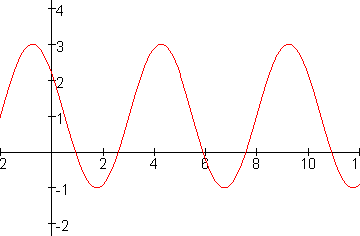
-
Stel een formule op van de vorm $y=a+b·\sin(c(x-d)$
|
Uitwerking opdracht 2
$ \large h(t) = a + b \cdot \sin \left( {c\left( {t - d} \right)} \right) $
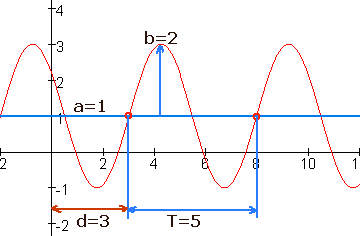
$
\large h(t) = 1 + 2 \cdot \sin \left( {\frac{{2\pi }}{5}\left( {t - 3} \right)} \right)
$
|
|
Opdracht 3

Stel een formule op van de vorm $y=a+b·\cos(c(x-d)$ |
Uitwerking opdracht 3
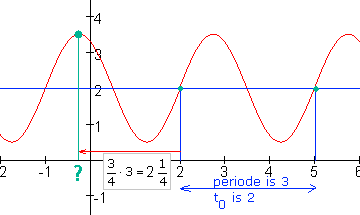
$
2 + 1,5\cos \left( {\frac{{2\pi }}{3}\left( {t + \frac{1}{4}} \right)} \right)
$
|
|
Opdracht 4

-
Stel een formule op van de vorm $y=a+b·cos(c(x-d)$
|
Uitwerking opdracht 4
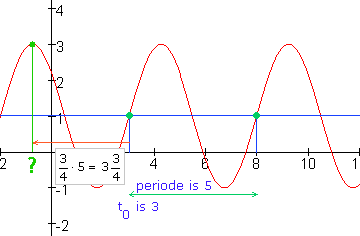
$
1 + 2\cos \left( {\frac{{2\pi }}{5}\left( {t + \frac{3}{4}} \right)} \right)
$
|
|
Opdracht 5
Gegeven is $f(x)=3sin(x)+2sin(x-\frac{1}{2}\pi)-1$
Schrijf met behulp van je GR $f$ in de vorm $y=a+bsin(c(x-d))$. Rond, zo nodig, af op 2 decimalen.
|
Uitwerking opdracht 5
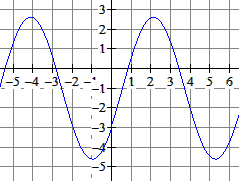
$y=-1+3,61·sin(x-0,59)$
|
|
Opdracht 6
Geef de evenwichtslijn, amplitude, periode en horizontale verschuiving van f:
$f(x)=3\sin(4x-1)+5$
|
Uitwerking opdracht 6
Zorg dat je de standaardformule gebruikt. Schrijf de functie als:
$f(x)=a+b·\sin(c(x-d))$
Bij dit voorbeeld wordt dat:
$f(x)=5+3·\sin(4(x-\frac{1}{4}))$
-
evenwichtslijn: y=5
-
amplitude = 3
-
periode = $\frac{2\pi}{4}=\frac{1}{2}\pi$
-
horizontale verschuiving=$\frac{1}{4}$
|
|
Opdracht 7
Op de kermis staat ‘n reuzenrad. Op ‘t hoogste punt is ‘n bakje 20 m boven de grond. Het rad maakt 2 omw/min. Op ‘t tijdstip t = 0 is ‘t bakje beneden.
-
Op welke hoogte is ‘t bakje na 10 sec?
|
Uitwerking opdracht 7
Evenwichtsstand=$10$
Amplitude=$10$
$\eqalign{c=\frac{2\pi}{0,5}=4\pi}$
Horizontale verschuiving=$0$
De 'slinger' begint op $0$ op $t=0$ dus neem $-\cos(...)$.
De formule is:
$H(t)=10-10·\cos(4\pi·t)$ met $t$ in minuten.
Na 10 seconden is de hoogte gelijk aan:
$\eqalign{H(t)=10-10·\cos(4\pi·\frac{10}{60})=15}$
Na 10 seconden bevindt 't bakje zich op 15 meter hoogte.
|















