|
De vermenigvuldigingregel
De vermenigvuldigingsregel gebruik je als handeling I op p manieren kan EN handeling II op q manieren kan. De gecombineerde handeling kan je dan op p×q manieren doen.
|
De somregel
De somregel gebruik je als handeling I op p manieren kan OF handeling II op q manieren kan. De gecombineerde handeling kan je dan op p+q manieren doen.
|
|
Voorbeeld 1
-
Je gooit 3 keer met een euro (kop of munt). Hoeveel verschillende uitkomsten zijn er ?
De eerste keer kun je kop of munt gooien, de tweede keer ook en de derde keer ook, dus zijn er $2^{3}=8$ mogelijkheden.
|
Voorbeeld 2
-
Bij een vereniging worden 3 mensen (A, B en C) in het bestuur gekozen die de functie van voorzitter, penningmeester en secretaris moeten vervullen. Op hoeveel manieren kan men deze 3 functies over deze 3 mensen verdelen?
Voor de voorzitter kan je kiezen uit drie, voor de penningmeester uit 2... Er zijn $3·2·1=6$ mogelijkheden.
|
|
Voorbeeld 3
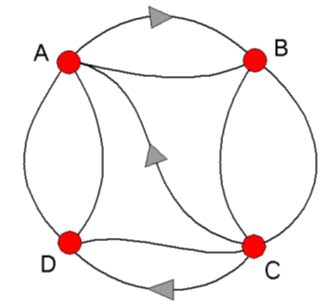
Je ziet hier een overzicht van fietspaden in een bosgebied. Er zijn vier mogelijke startpunten voor fietstochten: A, B, C en D. Sommige fietspaden zijn eenrichtingsverkeer. De mogelijke rijrichting is met een pijltje aangegeven.
-
Bart vertrekt in B en fietst via 2 fietspaden naar D. Op hoeveel manieren van dat?
Via A: op $1\cdot2=2$ manieren
Via C: op $2\cdot2=4$ manieren
In totaal kan Bart op $2+4=6$ manieren in twee stappen van B naar D.
|
|







