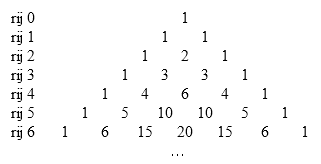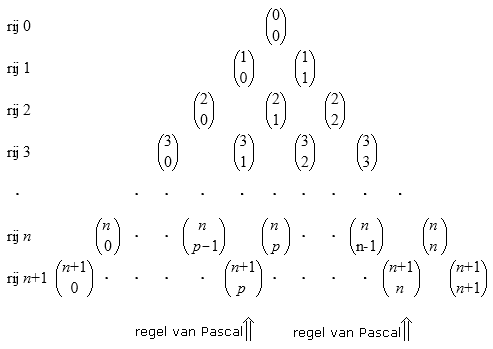|
De driehoek van Pascal
Elk getal in de driehoek van Pascal geeft het aantal kortste routes om vanuit de top op die plaats te komen.
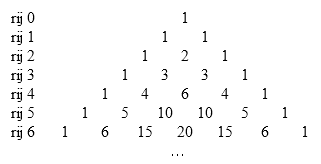
De getallen in de $n$-de rij zijn:
$
\left( {\begin{array}{*{20}c}
n\\
0\\
\end{array}} \right),\left( {\begin{array}{*{20}c}
n\\
1\\
\end{array}} \right),\left( {\begin{array}{*{20}c}
n\\
2\\
\end{array}} \right),...,\left( {\begin{array}{*{20}c}
n\\
n\\
\end{array}} \right)
$
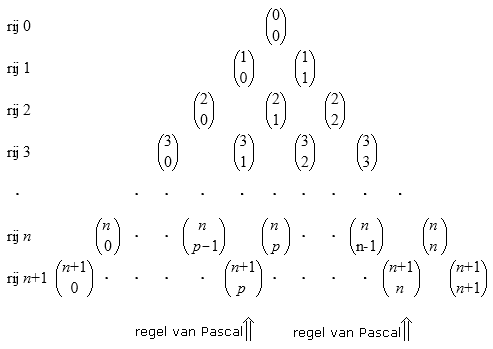
De som van de getallen in de $n$-de rij is $2^n$
De regel van Pascal
In de driehoek van Pascal is elk getal de som van de twee getallen die er schuin boven staan.
$
\left( {\begin{array}{*{20}c}
n\\
{k-1}\\
\end{array}} \right) + \left( {\begin{array}{*{20}c}
n\\
k\\
\end{array}} \right) = \left( {\begin{array}{*{20}c}
{n+1}\\
k\\
\end{array}} \right)
$
|
Sigma-notatie
Met het wiskundige symbool $\Sigma$ kunnen we (oneindige) reeksen kort opschrijven. De letter $\Sigma$ is de hoofdletter S uit het Griekse alfabet. Het symbool $\Sigma$ is een somteken (en heeft dus alles te maken met optellen):
De formule $
\sum\limits_{k = 1}^\infty {\frac{1}{{2^k }}}
$ staat voor de oneindige som $
\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + ...
$. Voor elk getal $
k = 1,\,\,2,\,\,3,\,\,...
$ tel je de breuken bij elkaar op.
$
\sum\limits_{k = 1}^5 k = 1 + 2 + 3 + 4 + 5 = 15
$
$
\sum\limits_{k = 0}^5 {\left( {\begin{array}{*{20}c}
5\\
k\\
\end{array}} \right) \cdot 2^k } = 3^5
$
$
\sum\limits_{k = 0}^n {\left( {\begin{array}{*{20}c}
n\\
k\\
\end{array}} \right)} = 2^n
$
$
\sum\limits_{k = 1}^\infty {\frac{1}{{2^k }}} = 1
$

|
|
Binomiaalcoëfficiënten
Bij het herleiden van $(a+b)^n$ komen de getallen van de $n$-de rij van Pascal tevoorschijn.
In het algemeen geldt:
$
\left( {a + b} \right)^n = \sum\limits_{k = 0}^n {\left( {\begin{array}{*{20}c}
n\\
k\\
\end{array}} \right)} \cdot a^{n - k} \cdot b^k
$
Deze formule heet het binomium van Newton. De getallen $
{\left( {\begin{array}{*{20}c}
n\\
k\\
\end{array}} \right)}
$ heten binomiaalcoëfficiënten.
Voorbeeld 1
Laat zien dat:
$
(x - 2)^3 = x^3 - 6x^2 + 12x - 8
$
Zie uitwerking
Voorbeeld 2
Geef de coëfficiënt van de vijfde term in de uitwerking van $(2p-3q)^7$.
Antwoord
Bij de vijfde term is $k=4$. Je krijgt dan:
$
\left( {\begin{array}{*{20}c}
7\\
4\\
\end{array}} \right) \cdot \left( {2p} \right)^3\cdot \left( { - 3q} \right)^4
$
Uitwerken geeft:
$
22680p^3 q^4
$
Het antwoord is $22680$
|
Multinomiaalcoëfficiënten
De coëfficiënten in de herleiding van een mulitonomium heten multinomiaalcoëfficiënten.
In de herleiding van $(p+q+r)^7$ is de binomiaalcoëfficiënt van $p^4q^2r$ gelijk aan:
$\left( {\begin{array}{*{20}c}
7\\
{4,2,1}\\
\end{array}} \right) $ = $\Large\frac{{7!}}{{4! \cdot 2! \cdot 1!}}$
De herleiding van $(p+q+r)^7$ kan met de sigma-notatie worden geschreven als:
$
(p + q + r)^7 = \sum\limits_{i + j + k = 7}^{} {\left( {\begin{array}{*{20}c}
7\\
{i,j,k}\\
\end{array}} \right)}\cdot p^i q^j r^k
$
...en dat is aan de vage kant:-)

|