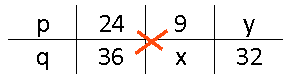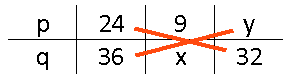|
Kruiselings vermenigvuldigen
In een verhoudingstabel gelden allerlei wetmatigheden. Een handige manier om 'onbekenden' uit te rekenen is met gebruik te maken van kruislings vermenigvuldigen.
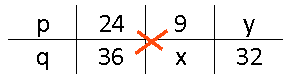 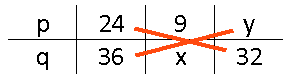

|
Rechthoekige driehoeken
Een rechthoekige driehoek heeft een rechte hoek, twee rechthoekszijden en een schuine zijde.
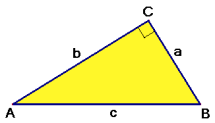
De rechthoekszijde $BC$ ligt tegenover $\angle A$. Daarom heet de zijde $BC$ de overstaande rechthoekszijde van $\angle A$.
De rechthoekszijde $AC$ is een been van $\angle A$. Zijde $AC$ heet de aanliggende rechthoekszijde van $\angle A$.
|
|
De stelling van Pythagoras
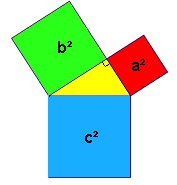
In een rechthoekige driehoek geldt:
a2+b2=c2
De schuine zijde in het kwadraat is gelijk aan de som van de kwadraten van de rechtshoekszijden.
|
Voorbeeld
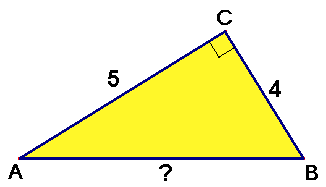
$
\angle
$C=90°, dus:
AC2+BC2=AB2
52+42=AB2
25+16=AB2
AB2=41
AB=$
\sqrt {41} \approx 6,4
$
|