|
Kwadratische vergelijkingen oplossen
Hoe los je de ongelijkheid $x^2-5\gt x+1$ op?
-
Neem $f(x)=x^2-5$ en $g(x)=x+1$
-
Los op $f(x)=g(x)$
-
Maak een schets van de grafieken en de snijpunten
-
Geef het antwoord
Voorbeeld
Los op: $x^2-5\gt x+1$
Uitwerking
$f(x)=x^2-5$ en $g(x)=x+1$
$f(x)=g(x)$
$x^2-5=x+1$
$x^2-x-6=0$
$(x-3)(x+2)=0$
$x=3$ of $x=-2$
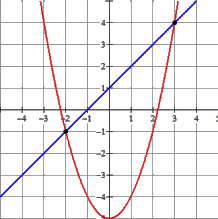
Antwoord: $x\lt-2$ of $x\gt3$
|
De ongelijkheden f(x)$\gt$0 en f(x)$\lt$0
Bij de ongelijkheid $f(x)\gt0$ is de vraag voor welke $x$ de grafiek van $f$ boven de $x$-as ligt. Je hebt dan de snijpunten van de grafiek van $f$ met de $x$-as nodig. Je begint met het oplossen van $f(x)=0$.
Voorbeeld
Los op: $(x-3)(x+2)\gt0$
-
Neem $f(x)=(x-3)(x+2)$. De nulpunten van $f$ zijn $x=-2$ en $x=3$. Het is een dalparabool dus de oplossing is:
$x\lt-2$ of $x\gt3$
Toepassing
Zie het voorbeeld op deze pagina.
Om de ongelijkheid $x^2-5\gt x+1$ op te lossen kan je de ongelijkheid ook eerst omwerken tot $f(x)\gt0$.
$x^2-5\gt x+1$
$x^2-x-5\gt 1$
$x^2-x-6\gt 0$
-
Neem $f(x)=x^2-x-6$
-
Los $f(x)=0$
$x^2-x-6=0$
$(x-3)(x+2)=0$
$x=-2$ of $x=3$
zie boven
Antwoord: $x\lt-2$ of $x\gt3$
|







