|
Vraag 1
Gegeven $\eqalign{f(x)=\frac{{x^3-1}}{x}}$
-
In welke punten is de richtingscoëfficiënt van de raaklijn gelijk aan 3?
Bereken eerst de afgeleide:
$
\eqalign{
&f(x)=\frac{{x^3-1}}
{x}\cr
&f(x)=\frac{{x^3}}
{x}-\frac{1}
{x}\cr
&f(x)=x^2-x^{-1}\cr
&f'(x)=2x--1\cdot x^{-2}\cr
&f'(x)=2x+\frac{1}
{{x^2}}\cr}
$
Voor welke waarde(n) voor $x$ is $f'(x)=3$?
$
\eqalign{
&2x+\frac{1}
{{x^2}}=3\cr
&2x^3+1=3x^2\cr
&2x^3-3x^2+1=0\cr
&oplossen\,\,met\,\,je\,\,GR:\cr
&x=-\frac{1}
{2}\vee x=1\cr}
$
Die punten zijn:
$\left({-\frac{1}{2},2\frac{1}{4}}\right),$ en $\left({1,0}\right)$.
|
Vraag 2
Gegeven $\eqalign{f(x)=\frac{{x^3-1}}{x}}$
-
Bereken de extreme waarde(n).
Extreme waarden:
$f'(x)=0$
$
\eqalign{
&2x+\frac{1}
{{x^2}}=0\cr
&2x^3+1=0\cr
&2x^3=-1\cr
&x^3=-\frac{1}
{2}\cr
&x=-\frac{1}
{{\root3\of2}}\cr}
$
Schets de grafiek:
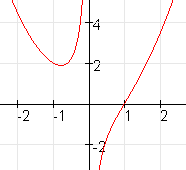
Een minimum bij $x=-\frac{1}
{{\root 3\of 2}}
$.
Het minimum is $1\frac{1}
{2}\root 3 \of 2
$
|







