|
1. en 2.
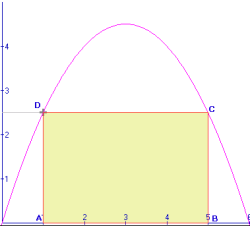
Druk AB en AD uit in $p$:
-
AB=$6-2p$
-
AD=$-0,5p^2+3p$
De omtrek van ABCD is gelijk aan 2·AB+2·AD. Je krijgt:
$O(p)=-p^2+2p+12$
De afgeleide is $O'(p)=-2p+2$.
Stel de afgeleide nul en los op:
$-2p+2=0$
$2p=2$
$p=1$
Plot de grafiek van $O(p)$. Is het een maximum, minumun of buigpunt?
De maximale omtrek is $O(1)=13$
|
3. en 4.
De oppervlakte van ABCD is gelijk aan AB·AD. Je krijgt:
$O(p)=p^3-9p^2+18p$
De afgeleide is $O'(p)=3p^2-18p+18$.
Stel de afgeleide op nul en los op:
$3p^2-18p+18=0$
$p^2-6p+6=0$.
$(p-3)^2-9+6=0$
$(p-3)^2-3=0$
$(p-3)^2=3$
$p-3=\pm\sqrt{3}$
$p=3\pm\sqrt{3}$
$p=3-\sqrt{3}$ of $p=3+\sqrt{3}$ (v.n.)
Plot de grafiek van $O(p)$. Is het een maximum, minimum of buigpunt?
De maximale oppervlakte is $O(3-\sqrt{3})=6\sqrt{3}$
|