|
Voorbeeld 1
Je hebt een rechthoekig stuk karton met afmetingen 80 cm bij 50 cm. Daaruit moet je een doos vouwen (zonder deksel!) met een zo groot mogelijke inhoud.
Je moet uit de vier hoeken van de rechthoek een stukje knippen om de doos te vormen.
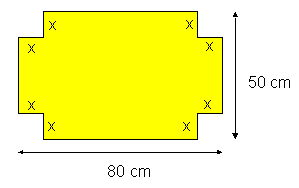
-
Bereken met de afgeleide hoe groot dat stukje moet zijn zodat de doos een maximale inhoud heeft.
|
Uitwerking
De inhoud van het doosje is gelijk aan de oppervlakte van het grondvlak maal de hoogte:
$I=G\cdot h=\left({80-2x}\right)\left({50-2x}\right)\cdot x$
Bepaal de afgeleide:
$\eqalign{&I=\left({80-2x}\right)\left({50-2x}\right)\cdot x\cr&I=\left({4000-160x-100x+4x^2}\right)\cdot x\cr&I=\left({4000-260x+4x^2}\right)\cdot x\cr&I=4000x-260x^2+4x^3\cr&I'=4000-520x+12x^2\cr}$
Neem O'(x)=0 en los de vergelijking op:
$\eqalign{&4000-520x+12x^2=0\cr&12x^2-520x+4000=0\cr&3x^2-130x+1000=0\cr&Met\,\,de\,\,abc-formule:\cr&x=\frac{{100}}{3}\vee x=10\cr}$
Maak een schets van de functie:
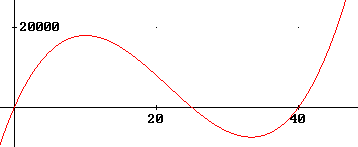
-
Bij $x=10$ heb je een maximum.
|








