|
Denkactiviteit
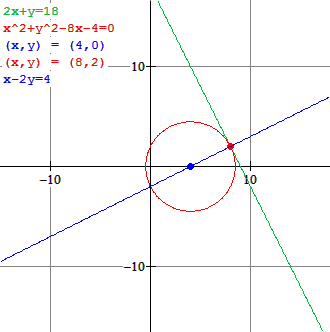
Bereken voor welke waarde van $a$ de lijn $k:2x+y=18$ raakt aan de cirkel $c:x^2+y^2-8x+a=0$.
Uitwerking
$ \begin{array}{l} \left\{ \begin{array}{l} 2x + y = 18 \\ x^2 + y^2 - 8x + a = 0 \\ \end{array} \right. \\ \left\{ \begin{array}{l} y = - 2x + 18 \\ x^2 + y^2 - 8x + a = 0 \\ \end{array} \right. \\ \left\{ \begin{array}{l} y = - 2x + 18 \\ x^2 + \left( { - 2x + 18} \right)^2 - 8x + a = 0 \\ \end{array} \right. \\ \left\{ \begin{array}{l} y = - 2x + 18 \\ x^2 + 4x^2 - 72x + 324 - 8x + a = 0 \\ \end{array} \right. \\ \left\{ \begin{array}{l} y = - 2x + 18 \\ 5x^2 - 80x + 324 + a = 0 \\ \end{array} \right. \\ D = ( - 80)^2 - 4 \cdot 5 \cdot \left( {324 + a} \right) \\ D = 6400 - 6480 - 20a \\ \left\{ \begin{array}{l} D = - 80 - 20a \\ D = 0 \\ \end{array} \right. \Rightarrow a = - 4 \\ \end{array} $
|