|
Populatiekenmerken
Bij een steekproevenverdeling is de steekproefproportie $\widehat p$ bij een voldoende grote steekproef $n$ bij benadering normaal verdeeld.
Hierbij is het gemiddelde $\mu$ gelijk aan de populatieproportie.
Voor de standaardafwijking $\sigma$ geldt:
$\eqalign{\sigma=\sqrt{\frac{\widehat p(1-\widehat p)}{n}}}$
Die $\widehat p$ is de steekproefproportie. Je kunt met $\widehat p$ een schatting doen van de populatieproportie. Die schatting is niet een waarde maar een interval waarbinnen met 68%- of 95%-betrouwbaarheid de populatieproportie ligt.
Bij nominale en ordinale variabelen kun je van elk van de voorkomende waarden de proportie berekenen.
Bij variabelen op interval- of rationiveau kan je het populatiegemiddelde schatten aan de hand van het steekproefgemiddelde. Daarbij bereken je ook betrouwbaarheidsintervallen.
|
Groepen vergelijken
Het weergeven van een verschil met een getal wordt kwantificeren van een verschil genoemd. Je zegt dan iets over de grootte van een verschil.
Bij variabelen van rationiveau zijn verschillen eenvoudig te berekenen. Of zo'n verschil dan klein, matig of groot is hangt af van de context maar in 't algemeen kan je daar wel iets zinnig over zeggen.
Verschillen kwatificieren bij nominale variabelen
1. Percentageverschil (PV)
2. Odds-ratio (OR)
3. De phi-coëfficiënt (phi)
Met de vuistregels kan je dan gebruiken om aan te bepalen of het verschil klein, matig of groot is.
De phi-coëfficient en de bijbehorende vuistregels staan op het formuleblad:
|
|
Betrouwbaarheidsintervallen voor populatiegemiddelde
Voor een populatiegemiddelde is:
het 68%-betrouwbaarheidsinterval:
$\eqalign{\left[ {\overline X - \frac{S}{{\sqrt n }},\overline X + \frac{S}{{\sqrt n }}} \right]}$
het 95%-betrouwbaarheidsinterval:
$\eqalign{\left[ {\overline X - 2 \cdot \frac{S}{{\sqrt n }},\overline X + 2 \cdot \frac{S}{{\sqrt n }}} \right]}$
Hierin is ${\overline X }$ het steekproefgemiddelde, $S$ de steekproefstandaardafwijking en $n$ de steekproefomvang.
Het 95%-betrouwbaarheidsinterval geeft aan dat het interval met 95% zekerheid het populatiegemiddelde bevat.
|
Verschillen kwantificeren bij ordinale variabelen
Voor het kwantificeren van een verschil bij ordinale variabele kan je kijken naar het maximale cumulatieve percentageverschil. Afgekort max.Vcp.
Met de vuistregels kun dan besluiten of het verschil klein, matig of groot is.
Zie ook het formuleblad.
Het berekenen van max.Vcp
-
Bereken voor de variabele het cumulatieve percentage.
-
Bereken bij elke categorie het verschil van de cumulatieve percentages.
-
Kijk wat het grootste verschil is dat optreedt, dat is de max.Vcp
|
|
Betrouwbaarheidsintervallen voor populatiegemiddelde in Excel
Voor het berekenen van een betrouwbaarheidsinterval voor een gemiddelde gebruik je in Excel de functie:
-
BETROUWBAARHEID($\alpha$,$S$,$n$)
De $\alpha$ is de onbetrouwbaarheid, bij 95% betrouwbaarheid is $\alpha$=0,05, de $S$ is de steekproefstandaardafwijking en $n$ is de steekproefgrootte.
Voorbeeld
Het gemiddelde wiskundecijfer in een steekproef van 31 leerlingen is 6,9. De standaarddeviatie is 2,0. Wat is dan het 90%-betrouwbaarheidsinterval?
Antwoord
-
Het 90%-betrouwbaarheidsinterval is [6,309;7,491]
|
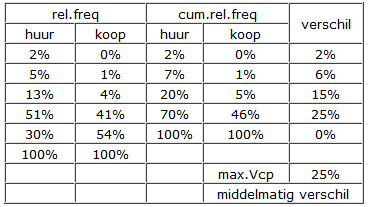
Voorbeeld max.Vcp
Bepaal voor de twee variabelen per categorie de relatieve cumulatie frequentie en bepaal het grootste verschil.
|








