|
De poissonverdeling
Er is sprake van een Poisson-verdeling als een kansexperiment met zeer kleine kans een groot aantal keren wordt uitgevoerd.
Volgens de Poisson-verdeling is de kans op $k$ keer succes gelijk aan:
$P(X=k)=e^{-\lambda}\cdot$ $\Large\frac{\lambda^{k}}{k!}$
Hierin is $\lambda$ het gemiddelde aantal keren succes.
Wat is e?
Die 'e' is het grondtal van de natuurlijke logaritme. Dat krijg je nog... $e\approx2,718$. Je kunt op je GR gebruik maken van de $e^{x}$-toets.
De Poisson-verdeling en je GR
Op je GR kan je benaderingen uitrekenen voor de kansen rondom de Poisson-verdeling.
|
Voorbeeld 1
In een bepaald gebied zijn er gemiddeld 4 blikseminslagen per jaar. Bereken de kans op 0, 1, 2, 3 of 4 blikseminslagen per jaar.
Met de formule kan je kansen $P(X=0)$, $P(X=1)$, ... uitrekenen. Bedenk daarbij dat $\lambda=4$.
$
\begin{array}{l}
P(X = 0) = e^{ - 4} \cdot \frac{{4^0 }}{{0!}} \approx 0,018 \\
P(X = 1) = e^{ - 4} \cdot \frac{{4^1 }}{{1!}} \approx 0,073 \\
P(X = 2) = e^{ - 4} \cdot \frac{{4^2 }}{{2!}} \approx 0,147 \\
\end{array}
$
...
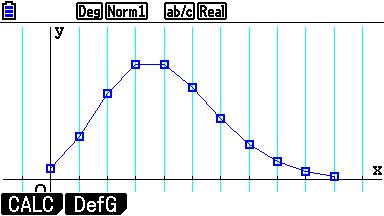
Uiteindelijk ziet dat er in een grafiek zo uit:
|
|
Voorbeeld 2
In een kerncentrale gebeurt gemiddeld 1 ongeval per jaar. Bereken de kans dat er
-
dit jaar 3 ongevallen gebeuren
-
hoogstens 3 ongevallen gebeuren
-
minstens 3 ongevallen gebeuren
|
Uitwerkingen voorbeeld 2
Met je GR via OPTN, STAT, DIST,  en POISSON
$\lambda=1$
-
$P(X=3)$=PoissonPD(3,1)$\approx0,061$
-
$P(X\le3)$=PoissonCD(3,1)$\approx0,981$
-
$P(X\ge3)$=1-PoissonCD(2,1)$\approx0,080$
|
