De optische vergelijking

Je hebt 2 muren met een onbekende ruimte ertussen. Nuu zijn er 2 planken die elkaar snijden, namelijk plank AC en plank BD.

$
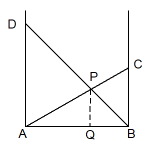
\eqalign{\frac{1}
{{AD}} + \frac{1}
{{BC}} = \frac{1}
{{PQ}}}
$

• Twee ladders

---

Dat geeft:

$
\eqalign{
  & \frac{1}
{h} = \frac{1}
{{20\sqrt 2 }} + \frac{1}
{{10\sqrt 3 }}  \cr
  & \frac{1}
{h} = \frac{{10\sqrt 3  + 20\sqrt 2 }}
{{20\sqrt 2  \cdot 10\sqrt 3 }}  \cr
  & h = \frac{{20\sqrt 2  \cdot 10\sqrt 3 }}
{{10\sqrt 3  + 20\sqrt 2 }}  \cr
  & h = \frac{{20\sqrt 6 }}
{{\sqrt 3  + 2\sqrt 2 }}  \cr
  & h = \frac{{20\sqrt 6 }}
{{\sqrt 3  + 2\sqrt 2 }} \cdot \frac{{\sqrt 3  - 2\sqrt 2 }}
{{\sqrt 3  - 2\sqrt 2 }}  \cr
  & h = \frac{{20\sqrt {18}  - 40\sqrt {12} }}
{{3 - 8}}  \cr
  & h = \frac{{60\sqrt 2  - 80\sqrt 3 }}
{{ - 5}}  \cr
  & h = 16\sqrt 3  - 12\sqrt 2  \cr}
$

Dat kan ook....

©2004-2024 W.v.Ravenstein