|
DifferentiequotiŽnt
De gemiddelde verandering van†$y$ op een interval is gelijk aan:
$
\Large \frac{{\Delta y}}
{{\Delta x}}
$
Voorbeeld
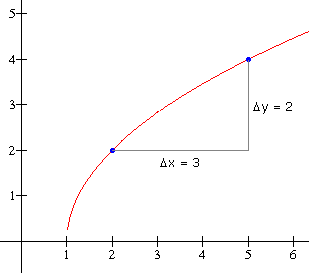
Op het interval $[2,5]$ is†$\Delta y = 2
$ en het differentiequotiŽnt is gelijk aan:
$
\Large\frac{{\Delta y}}{{\Delta x}} = \frac{{4 - 2}}{{5 - 2}} = \frac{2}{3}
$
|
RichtingscoŽfficiŽnt
Het differentiequotiŽnt van y op
$
\left[ {x_A ,x_B } \right]
$ is:
$
\Large \frac{{\Delta y}}
{{\Delta x}} = \frac{{y_B - y_A }}
{{x_B - x_A }}
$
De volgende begrippen komen op hetzelfde neer:
de gemiddelde verandering van y op $
\left[ {x_A ,x_B } \right]
$
het differentiequotiŽnt van y op $
\left[ {x_A ,x_B } \right]
$
de richtingscoŽfficiŽnt (helling) van de lijn AB
|
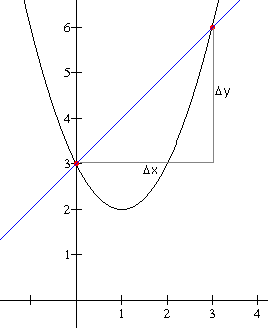
Formules
Bij de formule $y=x^{2}-2x+3$ bereken je het differentiequotiŽnt op $[0,3]$ als volgt:
$
\frac{{\Delta y}}{{\Delta x}} = \frac{{y(3) - y(0)}}{{3 - 0}} = \frac{{6 - 3}}{3} = 1
$
Met $A(0,3)$ en $B(3,6)$ geldt:
$rc_{AB}=1$†
†
|








