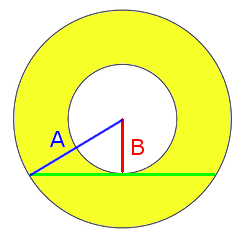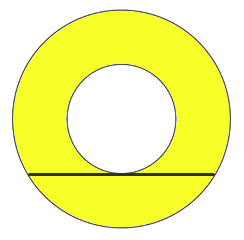
Een kermisklant moet het dek van een carrousel schilderen. Omdat het midden van ring geheel ingenomen wordt door de machinerie kan hij niet de diameter of de straal meten. Wat hij wel kan meten is de lengte van het groene lijnstuk. De lengte daarvan is 128 dm.

Bereken exact de oppervlakte van het ringvormige dek.

De oppervlakte van het ringvormige dek is gelijk aan:

$O=\pi A^{2}-\pi B^{2}=\pi(A^{2}-B^{2})$

Volgens de stelling van Pythagoras:

$A^{2}=B^{2}+64^{2}$ dus $A^{2}-B^{2}=64^{2}$

De oppervlakte is:

$O=4096\pi$