|
Voorbeeld 1
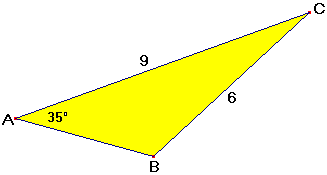
-
Bereken $\angle B$ in hele graden nauwkeurig.
|
Uitwerking
$
\begin{array}{l}
\frac{6}{{\sin 35^\circ }} = \frac{9}{{\sin \beta }} \\
6 \cdot \sin \beta = 9 \cdot \sin 35^\circ \\
\sin \beta = \frac{{9 \cdot \sin 35^\circ }}{6} \approx 0,860 \\
\beta \approx 59^\circ \,\,of\,\,\beta \approx 121^\circ \\
\end{array}
$
Die $59^o$ kan je goed zien als je $\Delta ABC$ gaat construeren.
|