De vergelijking en de normaalvector van een vlak

In het platte vlak heb je de assenvergelijking van een lijn. In de ruimte heb je een assenvergelijking voor een vlak.

Een assenvergelijking van het vlak $V$ door de punten
$P(p,0,0)$, $Q(0,q,0)$ en $R(0,0,r)$ is:

$V$:$\Large\frac{x}{p}+\frac{y}{q}+\frac{z}{r}$=$1$

Voorbeeld 1

$
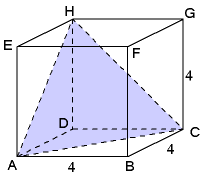
V:\frac{x}{4} + \frac{y}{4} + \frac{z}{4} = 1
$

$
V:x + y + z = 4
$

$
\underline n _V = \left( {\begin{array}{*{20}c}
1\\
1\\
1\\
\end{array}} \right) = \overrightarrow {DF}
$

 De normaalvector van een vlak

Een normaalvector van een vlak $V$ is een vector (ongelijk aan de nulvector) die loodrecht op $V$ staat.

De vector $
\underline n _V = \left( {\begin{array}{*{20}c}
a\\
b\\
c\\
\end{array}} \right)
$ is normaalvector van het vlak:

$V:ax+by+cz=d$

Voorbeeld 2

Is het vlak $U$ evenwijdig met de $y$-as en snijdt het vlak de $x$-as in het punt P(3,0,0) en z-as in het punt R(0,0,5), dan is:

$U:\frac{x}{3}+\frac{z}{5}=1$

Ofwel:

$U+5x+3z=14$

Dus:

$
\underline n _U  = \left( {\begin{array}{*{20}c}
5\\
0\\
3\\
\end{array}} \right)
$

Zie terugblik blz 83

Vlakken door de oorsprong

Bij het opstellen van een vergelijking van een vlak door de oorsprong ga je uit van de vergelijkingen:

$x+by+cx=0$

Immers.... het vlak gaat door de oorsprong

Bijzonder vlakken in een kubus

In een kubus:

• staat elke ribbe loodrecht op een zijvlak
• staat elke zijvlaksdiagonaal loodrecht op een diagonaalvlak
• staat elke lichaamsdiagobaal loodrecht op een vlak door drie hoekpunten dat niet een zijvlak of een diagonaalvlak is

Dit gebruik je om in een kubus snel een vergelijking van een vlak op te stellen.