De hoek tussen twee lijnen

In het platte vlak heb je al gerekend met het inproduct en de lengte van vectoren om de hoek tussen twee vectoren te berekenen.

In de ruimte gelden dezelfde regels:

Met $
\underline a = \left( {\begin{array}{*{20}c}
{a_1}\\
{a_2}\\
{a_3}\\
\end{array}} \right)
$ en $
\underline b = \left( {\begin{array}{*{20}c}
{b_1}\\
{b_2}\\
{b_3}\\
\end{array}} \right)
$ geldt:

$
\underline a\cdot \underline b = a_1 b_1 + a_2 b_2 + a_3 b_2
$

$
\begin{array}{l}
\left| {\underline a} \right| = \sqrt {a_1 ^2 + a_2 ^2 + a_3 ^2}\\
\left| {\underline b} \right| = \sqrt {b_1 ^2 + b_2 ^2 + b_3 ^2}\\
\end{array}
$
$
\cos \left( {\angle \left( {\underline a ,\underline b} \right)} \right) = \frac{{\underline a\cdot \underline b}}{{\left| {\underline a} \right|\cdot \left| {\underline b} \right|}}
$ met $
\underline a \ne \underline 0
$ en $
\underline b \ne \underline 0
$

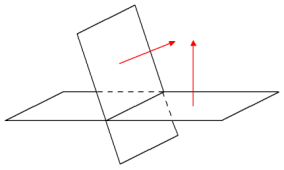
De hoek tussen twee vlakken

Een normaal van een vlak is een lijn die loodrecht op dat vlak staat. Een richtingsvector van een normaal is een normaalvector van het vlak.

De hoek tussen de vlakken $V$ en $W$ is de hoek tussen een normaal van $V$ en een normaal van $W$.

De hoek tussen een lijn en een vlak

Voor het berekenen van een de hoek $\varphi$ tussen een lijn $l$ en een vlak $V$ gebruik je een normaal $n$ van $V$.

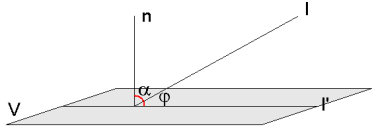
Bereken eerst $\alpha=\angle(l,n)$ en vervolgens $\varphi=90^o-\alpha$

Aanpak

Het berekenen van de hoek tussen een lijn $l$ met $
\underline r _l
$ en een vlak $V$ met $
\underline n _V
$:

1. Bereken een richtingsvector $
   \underline r _l
   $ van $l$ en een normaalvector $
   \underline n _V
   $ van $V$
2. Bereken $\angle(l,n)$ waarbij n een normaal is van $V$
3. Bereken $\angle(l,V)=90^o-\angle(l,n)$