Oppervlakten en normaalkrommen

Bij opgaven over oppervlakten onder de normaalkrommen spelen vijf getallen een rol:

1. het gemiddelde $\mu$
2. de standaardafwijking $\sigma$
3. de linkergrens $l$ van het gebied
4. de rechtergrens $r$ van het gebied
5. de oppervlakte van het gebied

Zijn er vier bekend dan kun je het vijfde getal berekenen.

Oppervlakten berekenen

Bij de normale verdeling met $\mu=178$ en $\sigma=8$ is de oppervlakte van het gebied onder de normaalkromme links van $168$ gelijk aan:

$NormalCD(-10^{99},168,8,178)\approx0,106$

Let op: deze volgorde wijkt af van de volgorde uit het boek.

• Zie De normale verdeling voor de berekeningen met de CASIO.

Grenzen berekenen

Als je de oppervlakte $A$ links onder de grafiek van $a$ weet dan kun je $a$ uitrekenen met InvNormCD.

Bij $A=0,25$, $\mu=178$ en $\sigma=8$ is $a$ gelijk aan:

$InvNorm(0.25,8,178)\approx172,6$

Let op: de volgorde is anders dan de volgorde in je boek.

• Zie De normale verdeling voor de berekeningen met de CASIO.

Tips en truuks...

• Gebruik, als het kan, altijd de 'normale' functies rondom de normaalverdeling. Deze werken beter en sneller dan de solver.
• Soms lukt het de solver niet om een oplossing te vinden terwijl er wel een oplossing moet zijn. Probeer in dat geval andere instellingen voor Lower en Upper in het solver-menu.
• Maak schetsen van de normaalkromme en zet de gegevens in je tekening.

Het berekenen van het gemiddelde of de standaarddeviatie

Met de SOLVER op je grafische rekenmachine kan je steeds 1 onbekende parameter bepalen.

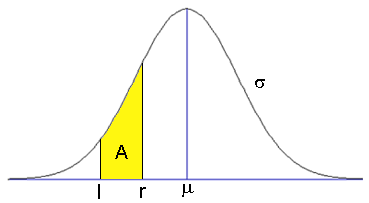
• $Eq:NormCD(l,r,\sigma,\mu)=A$

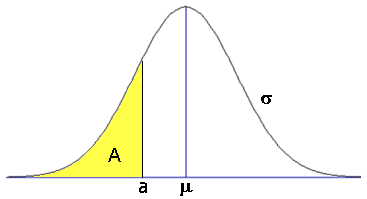
• $Eq:InvNormCD(A,\sigma,\mu)=a$

Zie F3: Solver

• voorbeelden