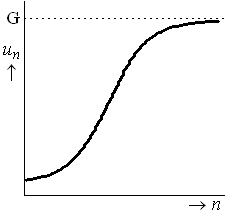
De grafiek bij logistische groei

• De formule is:
  $N=$ $\Large\frac{G}{1+b\cdot g^t}$
  Met $b\gt 0$ en $0\lt g\lt t$.
• Door invloeden van buitenaf vindt afremming van exponentiële groei plaats.
• De grafiek is een $S$-vormige kromme die voor grotere waarden van $t$ de grenswaarde nadert.
• De toenemende stijging duurt tot het tijdstip waarop de helft van de grenswaarde bereikt wordt.

Logistische groei aantonen

$N=$ $\Large\frac{G}{1+b\cdot g^t}$

• $G$ is de grenswaarde
• $N^*=$ $\Large\frac{G-N}{N}$ neem exponentieel af.
• $N^*=b\cdot g^t$

Voorbeeld

Bij een groei hoort de volgende tabel:

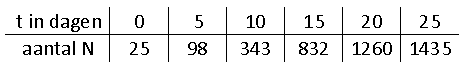
Toon aan dat bij deze tabel logistische groei met grenswaarde 1500 hoort en stel de bijbehorende formule op.

Uitwerking voorbeeld blz 175

Begrensde groei

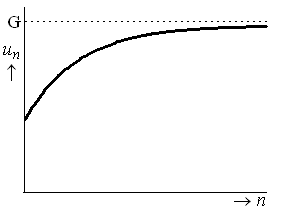
Bij begrensde groei met $0\lt g \lt 1$ en grenswaarde $G$ hoort de formule:

$N=G(1-g^t)$

In tegenstelling tot logistische groei is de hele grafiek afnemend stijgend.

Extra

• Bij exponentiële groei is de groeisnelheid evenredig met de aanwezige hoeveelheid.

• Bij begrensde groei is de groeisnelheid evenredig met het verschil tussen de hoeveelheid en een bovengrens.

• Bij logistische groei is de groeisnelheid afhankelijk van de aanwezige hoeveelheid als ook van een remfactor.