Constructie

Snijdt $CP$ met de $z$-as in $R$. Snijdt $RA$ met $EH$ en teken $T$. Teken $PT$ en $AC$.

Teken het vlak $DBFH$ en teken de snijlijn $VW$ van $ACPE$ en $DBFH$.

Snijdt $DF$ met $VW$ en je hebt het snijpunt $S$ gevonden.

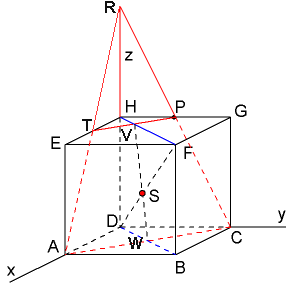
Berekening

Teken de doorsnede $DBFH$:

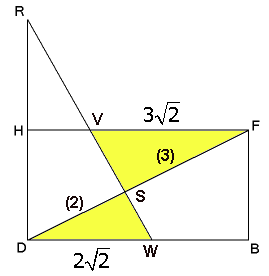
Bereken de lengte van $VF$ en $DW$. Het punt $S$ ligt op $\frac{2}{5}$ van $DF$.

$\overrightarrow {DS} = \frac{2}{5}\left( {\begin{array}{*{20}c} 4\\ 4\\ 4\\ \end{array}} \right) = \left( {\begin{array}{*{20}c} {1\frac{3}{5}}\\ {1\frac{3}{5}}\\ {1\frac{3}{5}}\\ \end{array}} \right)$

$S\left( {1\frac{3}{5},1\frac{3}{5},1\frac{3}{5}} \right)$