Voorwaardelijke theoretische kansen

$P(B | A)$ is de kans op $B$ onder de voorwaarde $A$.

$
P\left( {B|A} \right)$=$\Large\frac{{P\left( {A \cap B} \right)}}{{P\left( A \right)}}
$ waarbij $
P\left( A \right) \ne 0
$

Voorbeeld 1

In een onderzoek onder 185 studenten, blijken er 91 geschiedenis te studeren en 75 biologie. 37 studenten doen beiden.

We onderscheiden de volgende gebeurtenissen:

• $G$: student studeert geschiedenis
• $B$: student studeert biologie

Bereken $P(G|B)$ en $P(B|G)$

Antwoord

$
P\left( {G \cap B} \right) = \frac{{37}}{{185}}
$, $
P\left( G \right) = \frac{{91}}{{185}}
$ en $
P\left( B \right) = \frac{{75}}{{185}}
$

$
\begin{array}{l}
 P\left( {G|B} \right) = \frac{{\frac{{37}}{{185}}}}{{\frac{{75}}{{185}}}} = \frac{{37}}{{75}} \approx {\rm{0}}{\rm{,493}} \\
 {\rm{P}}\left( {B|G} \right) = \frac{{\frac{{37}}{{185}}}}{{\frac{{91}}{{185}}}} = \frac{{37}}{{91}} \approx {\rm{0}}{\rm{,407}} \\
 \end{array}
$

Onafhankelijke gebeurtenissen

$A$ en $B$ zijn onafhankelijke gebeurtenissen betekent:

$P(A|B)=P(A)$

Voorbeeld 2

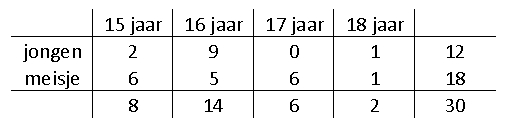
We onderscheiden de volgende gebeurtenissen:

• $A$: leerlingen is een jongen
• $B$: leerling is 15 of 16 jaar

Bereken $P(A|B)$ en $P(A)$. Welke conclusie kun je daar uit trekken?

Antwoord

$P(A|B)=\frac{11}{22}=\frac{1}{2}$ en $P(A)=\frac{12}{30}=\frac{2}{5}$. De gebeurtenissen $A$ en $B$ zijn niet onafhankelijk.

De regel van Bayes

Voor de gebeurtenissen $A$ en $B$ bij een kansexperiment geldt:

$
P\left( {B|A} \right)
$=$
\Large\frac{{P\left( {A|B} \right) \cdot P\left( B \right)}}{{P\left( A \right)}}
$

Voorbeeld 1

Van een groep van 1000 studenten gaat 20% op wintersport. Van de studenten die op wintersport gaan komt 1% terug met een been in het gips. In totaal zijn er 4 studenten met een been in 't gips.

• Hoeveel procent van de studenten die zijn been gebroken heeft is op wintersport geweest?

Antwoord voorbeeld 1

$
\begin{array}{l}
 P\left( {B|A} \right) = \frac{{P\left( {A|B} \right) \cdot P\left( B \right)}}{{P\left( A \right)}} \\
 A:breekt\,\,been \\
 B:gaat\,\,op\,\,w{\mathop{\rm int}} ersport \\
 P(A|B) = \frac{2}{{200}} = 0,01 \\
 P(B) = \frac{{200}}{{1000}} = 0,2 \\
 P(A) = \frac{4}{{1000}} = 0,004 \\
 P(B|A) = \frac{{0,01 \cdot 0,2}}{{0,004}} = 0,5 \\
 \end{array}
$
Van de studenten die hun been gebroken hebben is 50% op wintersport geweest....

Wow:-)