|
Voorbeeld
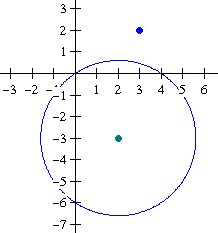
Geef de raaklijnen van
$c:(x-2)^2+(y+3)^2=13$
die door $B(3,2)$ lopen.
|
Uitgewerkt
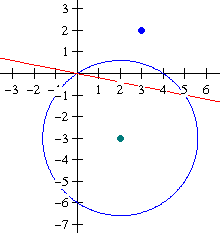
De poollijn: $p:(3-2)(x-2)+(2+3)(y+3)=13$ ofwel $p:x+5y=0$
$
\begin{array}{l}
\left\{ \begin{array}{l}
(x - 2)^2 + (y + 3)^2 = 13\\
x + 5y = 0\\
\end{array} \right. \\
( - 5y - 2)^2 + (y + 3)^2 = 13 \\
25y^2 + 20y + 4 + y^2 + 6y + 9 = 13 \\
26y^2 + 26y = 0 \\
y^2 + y = 0 \\
y(y + 1) = 0 \\
\left\{ \begin{array}{l}
y = 0 \\
x = 0 \\
\end{array} \right. \vee \left\{ \begin{array}{l}
y = - 1 \\
x = 5 \\
\end{array} \right. \\
\end{array}
$
Raaklijn door $(0,0)$:
$(0-2)(x-2)+(0+3)(y+3)=13$
$-2x+4+3y+9=13$
$-2x+3y=0$
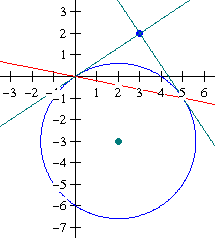
Raaklijn door $(5,-1)$
$(5-2)(x-2)+(-1+3)(y+3)=13$
$3x-6+2y+6=13$
$3x+2y=13$
|