|
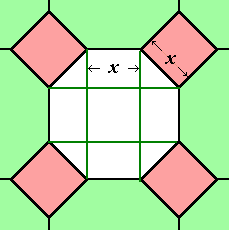
De achthoek bestaat uit 4 driehoeken, 4 rechthoeken en 1 vierkant.
$
\eqalign{
& driehoeken:4 \cdot \frac{1}
{2}\left( {\frac{1}
{2}\sqrt 2 \cdot x} \right)^2 = x^2 \cr
& rechthoeken:4 \cdot \frac{1}
{2}\sqrt 2 \cdot x \cdot x = 2\sqrt 2 \cdot x^2 \cr
& vierkant:x^2 \cr
& (2 + 2\sqrt 2 )x^2 = 6 \cr
& x^2 = \frac{3}
{{1 + \sqrt 2 }} = 3\sqrt 2 - 3 \cr}
$
De oppervlakte van zo'n vierkant is $
3\sqrt 2 - 3
$ cm².
ps
$
\eqalign{
\frac{3}
{{1 + \sqrt 2 }} \cdot \frac{{1 - \sqrt 2 }}
{{1 - \sqrt 2 }} = \frac{{3 - 3\sqrt 2 }}
{{1 - 2}} = 3\sqrt 2 - 3}
$
|