De tangens van een hellingshoek

Als je bij een hellingshoek van $31^o$ het hellingsgetal berekent dan komt daar ongeveer $0,6$ uit. Dat staat los van de afmetingen van de driehoek. Kennelijk hoort er bij een hoek een bepaalde waarde van het hellingsgetal.

In plaats van hellingsgetal gebruiken we tangens. Je kunt zeggen dat de tangens van een hoek van $31^o$ ongeveer gelijk is aan $0,6$.

$
\eqalign{{\rm{tan(hellingshoek) = }}{{{\rm{verticale verplaatsing}}} \over {{\rm{horizontale verplaatsing}}}}}
$

Op je rekenmachine kan je een knopje vinden waarmee je voor een willekeurige hellingshoek de waarde van de tangens kunt benaderen. Er is ook een knopje om de hoek te berekenen als je de tangens weet.

Van hellingsgetal naar hellingshoek v.v.

Gebruik de volgende functies op je rekenmachine:

Welke tangens hoort er bij een hoek van $38^o$?

• $tan(38)\to0,781$

Welke hoek hoort er bij een tangens van $0,333$?

• $0,333\to18,4^o$

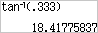
Spreek $tan^{-1}$ uit als 'inverse tangens'.

Tangens en verhoudingstabel

De tangens is een voorbeeld van een goniometrische verhouding.

Dat wil zeggen dat de waarde van de tangens de verhouding geeft van de twee rechthoekszijden van een rechthoekige driehoek.

Omdat de tangens een verhouding aangeeft kan je bij berekeningen gebruik maken van een verhoudingstabel.

Voorbeeld

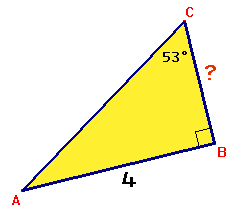
$\angle C=53^o$ en $AB=4$. In een verhoudingtabel wordt dat:

Met kruislings vermenigvuldigen kan je waarde van $BC$ berekenen.

$tan(53^o)\times BC=1\times4$
$\eqalign{BC=\frac{4}{tan(53^o)}\approx3}$

Afspraak

• Als er niet expliciet iets anders gevraagd wordt dan bereken je hoeken op 1 decimaal nauwkeurig.