|
Combinaties
Als je $k$ dingen kiest uit $n$ waarbij de volgorde er niet toe doet en herhalingen niet zijn toegestaan, dan het je maken met een combinatie.
Notatie: $
\left( {\begin{array}{*{20}c}
n\\
k\\
\end{array}} \right)
$
Spreek uit als 'n boven k'.
Voorbeeld
Je kiest 6 leerlingen uit een klas van 20 voor een volleyball team. Op hoeveel manieren kan dat?
$
\left( {\begin{array}{*{20}c}
{20}\\
6\\
\end{array}} \right) = {\rm{38}}{\rm{.760}}
$
|
Herhalingscombinaties
Als je $k$ dingen kiest uit $n$ waarbij de volgorde er niet toe doet en herhaling wel zijn toegestaan dan heb je te maken met een herhalingscombinatie.
Voorbeeld
Je verdeelt 32 rode rozen over 3 vazen waarbij in elke vaas minstens 5 rozen moeten komen. Om hoeveel manieren kan de rozen verdelen over de vazen?
Zet in elke vaas 5 rozen. Verdeel de overgebleven 17 rozen over de 3 vazen. Dit is een herhalingscombinatie van 17 keer kiezen uit 3.
$
\left( {\begin{array}{*{20}c}
{3-1+17}\\
17\\
\end{array}} \right) = \left( {\begin{array}{*{20}c}
{19}\\
17\\
\end{array}} \right) = 171
$
|
|
Het aantal combinatie van $k$ uit $n$ is gelijk aan:
$
\left( {\begin{array}{*{20}c}
n\\
k\\
\end{array}} \right)
$=$
\Large\frac{{n!}}{{k! \cdot \left( {n - k} \right)!}}
$
Zie grafische rekenmachine
|
Aantal herhalingscombinaties van $k$ uit $n$ is gelijk aan:
$
\left( {\begin{array}{*{20}c}
{n-1+k}\\
k\\
\end{array}} \right)
$
Zie waar komt die formule vandaan?
|
|
Het aantal kortste routes in een p×q-rooster van het ene hoekpunt naar het overstaande hoekpunt is:
$
\left( {\begin{array}{*{20}c}
{p+q}\\
p\\
\end{array}} \right)
$
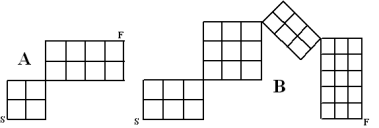
|
$
\begin{array}{l}
A.\\
\left( {\begin{array}{*{20}c}
4\\
2\\
\end{array}} \right) \times \left( {\begin{array}{*{20}c}
6\\
4\\
\end{array}} \right) = 90 \\
B.\\
\left( {\begin{array}{*{20}c}
5\\
3\\
\end{array}} \right) \times \left( {\begin{array}{*{20}c}
6\\
3\\
\end{array}} \right) \times \left( {\begin{array}{*{20}c}
5\\
3\\
\end{array}} \right) \times \left( {\begin{array}{*{20}c}
8\\
5\\
\end{array}} \right) = 112.000 \\
\end{array}
$ |