|
Wat is kans?
"kans, v.(m.) -en (gew. Fra. chance [Lat. cadentia = het vallen]: 1 mogelijkheid, inz.waarschijnlijkheid; 2 uitzicht op geluk; 3 gunstige gelegenheid): "
Wiskundig gezien is kans een getal tussen 0 en 1 dat aangeeft hoe (on)waarschijnlijk een bepaalde gebeurtenis is. Een 0 betekent dat het waarschijnlijk niet gebeurt en een 1 betekent dat het vrijwel zeker gebeurt. In de praktijk kun je alle waarden tussen 0 en 1 tegenkomen.
Een voorbeeld van een kans van 0:
· De kans dat pasen en pinksteren op één dag vallen
Een voorbeeld van een kans van 1:
· De kans dat eerste kerstdag op 25 december valt
In het algemeen maakt men onderscheid tussen experimentele en theoretische kansen. Theoretische kansen kun je (in principe) uitrekenen. Experimentele kansen kun je te weten komen door experimenten uit te voeren of door het verzamelen van statistisch materiaal.
|
Kansen berekenen
De kans op gebeurtenis G is gelijk aan:
$
P(G) = \frac{{{\rm{gunstige}}\,\,{\rm{uitkomsten}}}}{{{\rm{mogelijke}}\,\,{\rm{uitkomsten}}}}
$
Voorwaarde is dat de kansen op alle mogelijke uitkomsten gelijk zijn.
Voorbeeld 1
Je gooit met een eerlijke dobbelsteen. De kans dat je meer dan 4 ogen gooit is gelijk aan:
$
P(k > 4) = \frac{{\rm{2}}}{{\rm{6}}} = \frac{1}{3}
$
Voorbeeld 2
Je gooit met 3 munten, wat is de kans op 3 keer kop?
$
P(3\,\,kop) = \frac{{\rm{1}}}{{\rm{8}}}
$
|
|
Een rooster maken bij twee experimenten
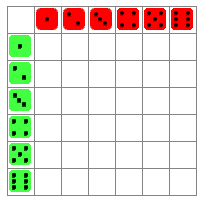
Bij 't gooien van twee dobbelstenen, het gooien met twee geldstukken of bij het draaien van twee kanstolletjes kan je alle mogelijke (en gunstige) uitkomsten in een rooster zetten.

|
Samengestelde kansexperimenten met meer dat twee experimenten
Je kunt de kansen berekenen door:
-
Bereken het aantal mogelijke uitkomsten
-
Tel het aantal gunstige uitkomsten door systematisch te noteren en/of te tellen
-
Deel het aantal gunstige uitkomsten door het aantal mogelijke uitkomsten
Voorbeeld
Je gooit met 3 dobbelstenen. Wat is de kans dat je in totaal zes ogen gooit?
-
Aantal mogelijk: $6^{3}=216$
-
Aantal gunstig: er zijn $10$ manieren om $6$ ogen te gooien.
Zie telproblemen visualiseren
-
De kans is:
$
P(6\,\,ogen) = \frac{{{\rm{10}}}}{{{\rm{216}}}} = \frac{5}{{108}}
$
|