Weet, zweet en zwetskansen

Een 'weetkans' is een theoretische kans die je kan uitrekenen. Bijvoorbeeld de kans om 3 te gooien bij een eerlijke dobbelsteen.

Een 'zweetkans' is een kans die je niet kan 'raden' maar moet onderzoeken. Dat is hoop werk...

Een 'zwetskans' een kans waar je niks van weet maar je roept maar wat. De kans dat het morgen regent is 20%. Dat kan best kloppen, maar meestal is het onzin.

Empirische kansen

Door een kansexperiment heel vaak uit te voeren komt de relatieve frequentie van een gebeurtenis dichtbij de kans op de gebeurtenis te liggen.
(wet van de grote aantallen)

Empirische kansen kan je benaderen met de relatieve frequenties.

Voorwaardelijke kansen

De voorwaardelijke kans $P(A | B)$ is de kans op $A$ onder de voorwaarde $B$:

Er geldt:

$P\left( {A|B} \right)$ = $\Large\frac{{\# \left( {A \cap B} \right)}}{{\# \left( B \right)}}
$

Je spreekt $P(A|B)$ uit als 'de kans op A onder de voorwaarde B'.

Bij een voorwaardelijke kans beperk je je tot een doelgroep. Je moet dan delen door de frequentie van die deelgroep.

Afspraak

Bereken kansen in 3 decimalen, tenzij iets anders gevraagd wordt.

Voorbeeld

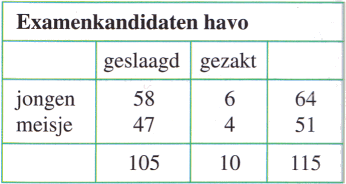
1. Wat is de kans dat een jongen geslaagd is?
2. Wat is de kans dat een meisje geslaagd is?
3. Wat is de kans dat een willekeurig gekozen examenkandidaat geslaagd is?

Zie uitwerking

Kansen bij kruistabellen

Voor een ziekte waar 1 op de 1000 mensen aan lijdt, is een 99% betrouwbare test ontwikkeld. Wat is de kans dat je ook echt ziek bent als de test dat uitwijst?

Zie uitwerking2

Voorbeeld 2

In een onderzoek onder 185 studenten, blijken er 91 geschiedenis te studeren en 75 biologie. 37 studenten doen beiden. Hoeveel studenten studeren precies één van de twee vakken?

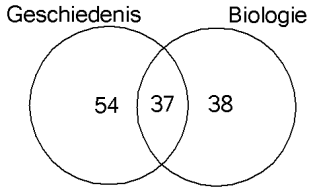
Antwoord: 92 studenten studeren één vak.

Voorbeeld 3

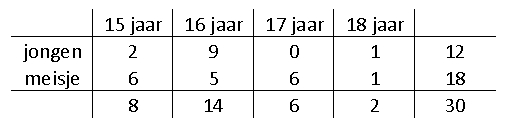
• P(dat een 16 jarige een meisje is)=$\large\frac{5}{14}$
• P(een meisje of 15 jaar)=$\large\frac{20}{30}$