|
Knikkers uit een vaas
In een vaas zitten 12 witte en 8 rode knikkers. Je pakt hieruit 4 knikkers zonder terugleggen. Wat is de kans op 3 witte knikkers?
Antwoord
Als je niet op de volgorde let, dan zijn er
$
\left( {\begin{array}{*{20}c}
{12} \\
3 \\
\end{array}} \right)
$ manieren om 3 van de 12 witte knikkers te pakken.
Er zijn $
\left( {\begin{array}{*{20}c}
8 \\
1 \\
\end{array}} \right)
$ manieren om 1 van de 8 rode knikkers te pakken.
In totaal zijn er dus $
\left( {\begin{array}{*{20}c}
{12} \\
3 \\
\end{array}} \right) \cdot \left( {\begin{array}{*{20}c}
8 \\
1 \\
\end{array}} \right)
$ manieren om 3 witte en 1 rode knikker uit de vaas te pakken.
In totaal zijn er $
\left( {\begin{array}{*{20}c}
{20} \\
4 \\
\end{array}} \right)
$ manieren om 4 knikkers uit de vaas te pakken.
P(3 wit en 1 rood)=$
\frac{{\left({\begin{array}{*{20}c}
{12}\\
3\\
\end{array}}\right)\cdot\left({\begin{array}{*{20}c}
8\\
1\\
\end{array}}\right)}}{{\left({\begin{array}{*{20}c}
{20}\\
4\\
\end{array}}\right)}}=\Large\frac{{352}}{{969}}
$
|
Meerdere kleuren
In een vaas zitten 5 rode, 4 groene en 1 blauwe knikker. Je pakt 3 knikkers uit de vaas zonder terugleggen. Bereken de kans op 3 verschillende kleuren.
Antwoord
$P(X=3)=\frac{{\left( {\begin{array}{*{20}c}
5\\
1\\
\end{array}} \right)\left( {\begin{array}{*{20}c}
4\\
1\\
\end{array}} \right)\left( {\begin{array}{*{20}c}
1\\
1\\
\end{array}} \right)}}{{\left( {\begin{array}{*{20}c}
{10}\\
3\\
\end{array}} \right)}} = \frac{1}{6}
$
Voorbeeld
Bij een loterij zijn 40 loten verkocht. Er zijn 3 eerste prijzen en 7 tweede prijzen. Je koopt 3 loten.
-
Bereken de kans op 1 eerste prijs en 2 tweede prijzen.
Antwoord
$
P(G) = \frac{{\left( {\begin{array}{*{20}c}
3\\
1\\
\end{array}} \right) \cdot \left( {\begin{array}{*{20}c}
7\\
2\\
\end{array}} \right)}}{{\left( {\begin{array}{*{20}c}
{40}\\
3\\
\end{array}} \right)}} \approx 0,006
$
|
|
Kansbomen en de productregel
Kansexperimenten die uit twee of meer experimenten bestaan die elkaar op geen enkele manier beinvloeden heten onafhankelijke kansexperimenten.
Je kunt daarbij gebruik maken van een kansboom. De kansen langs de takken kan je dan vermenigvuldigen.
Voorbeeld:
Je gooit met een munt en een dobbelsteen.
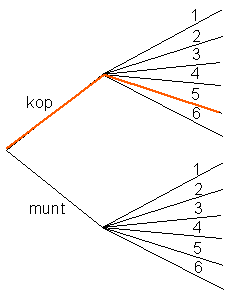
Gebeurtenis $A$: je gooit met de munt kop
Gebeurtenis $B$: je gooit 5 ogen met de dobbelsteen
De gebeurtenissen $A$ en $B$ zijn onafhankelijk.
|
Onafhankelijke gebeurtenissen
Twee gebeurtenissen $A$ en $B$ zijn onafhankelijk als:
$
P\left( {A \cap B} \right) = P\left( A \right) \cdot P\left( B \right)
$
In het voorbeeld van de 'munt en de dobbelsteen' geldt:
$P(A)$=$\frac{1}{2}$
$P(B)$=$\frac{1}{6}$
$P(A\cap B)$=$\frac{1}{12}$
Iets anders...
-
Wat zou $P(A\cup B)$ zijn?
Iemand geeft als antwoord:
De kans op kop is een $\frac{1}{2}$, de kans op vijf is $\frac{1}{6}$. Het is een OF-kans, dus de kans op een kop of vijf is gelijk aan $\frac{1}{2}+\frac{1}{6}=\frac{2}{3}$. Denk maar aan de somregel.
-
Welke 'denkfout' maakt deze persoon?
HINT
$
P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {A \cap B} \right)
$
|