Je ziet hier een graaf met de punten $A$, $B$ en $C$. Er zijn tussen de punten verschillende wegen. Sommige van die wegen zijn éénrichtingsverkeer.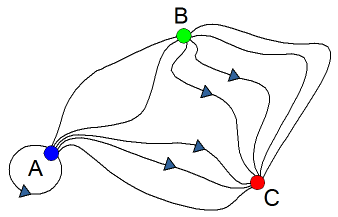

Je kunt bij deze graaf een directe-wegen-matrix opstellen. Hierin kan je dan aangeven hoeveel directe verbindingen er zijn tussen de verschillende punten. Dat ziet er dan zo uit:

$\begin{array}{*{20}c}M&{\begin{array}{*{20}c}{van}\\{\begin{array}{*{20}c}A&B&C\\\end{array}}\\\end{array}}\\{\begin{array}{*{20}c}{naar}&{\begin{array}{*{20}c}A\\B\\C\\\end{array}}\\\end{array}}&{\left({\begin{array}{*{20}c}1&2&1\\2&0&2\\3&4&0\\\end{array}}\right)}\\\end{array}$

Er zijn (bijvoorbeeld) 4 directe wegen van $B$ naar $C$, maar er zijn 2 directe wegen van $C$ naar $B$.

M in het kwadraat

Je kunt $M$ met zichzelf vermenigvuldigen:

$M^2=\left({\begin{array}{*{20}c}1&2&1\\2&0&2\\3&4&0\\\end{array}}\right)\times\left({\begin{array}{*{20}c}1&2&1\\2&0&2\\3&4&0\\\end{array}}\right)=\left({\begin{array}{*{20}c}8&6&5\\8&{12}&2\\{11}&6&{11}\\\end{array}}\right)$

Dat geeft:

$\begin{array}{*{20}c}{M^2}&{\begin{array}{*{20}c}{van}\\{\begin{array}{*{20}c}A&B&C\\\end{array}}\\\end{array}}\\{\begin{array}{*{20}c}{naar}&{\begin{array}{*{20}c}A\\B\\C\\\end{array}}\\\end{array}}&{\left({\begin{array}{*{20}c}8&6&5\\8&{12}&2\\{11}&6&{11}\\\end{array}}\right)}\\\end{array}$

De getallen in $M^2$ geven het aantal tweestapswegen. Hoe kan je dat controleren?

Volgens matrix $M^2$ zijn er $8$ tweestapswegen van $A$ naar $A$. Dit getal komt van deze vermenigvuldiging (rij×kolom):

$1·1 + 2·2 + 1·3 = 1 + 4 + 3 = 8$

Wat reken je dan precies uit?

• Er is $1$ manier om van $A$ naar $A$ te gaan. Er zijn dan $1·1=1$ manieren om in twee stappen van $A$ naar $A$ te gaan.
• Er zijn $2$ manieren om van $A$ naar $B$ te gaan en er zijn $2$ manieren om van $B$ naar $A$ te gaan. Om in twee stappen van $A$ naar $A$ te gaan (via $B$) kan dan op $2·2=4$ manieren.
• Er zijn $3$ manieren om van $A$ naar $C$ te gaan en er is $1$ manier om van $C$ naar $A$ te gaan. Om in twee stappen van $A$ naar $A$ te gaan (via $C$) kan dan op 1·3=3 manieren.

In totaal kan je dus op 1+4+3=8 manieren van $A$ naar $A$ in twee stappen.

• 't Is een nuttige oefening om die 8 routes even na te lopen...