|
Een algemene manier om de determinant van een matrix te berekenen, vind je op:
Een vlotte manier om van een 3x3 matrix de determinant te berekenen, is de volgende:
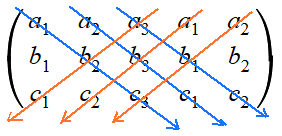
$\left({\begin{array}{*{20}c}{a_1}&{a_2}&{a_3}\\{b_1}&{b_2}&{b_3}\\{c_1}&{c_2}&{c_3}\\\end{array}}\right)$ $\left({\begin{array}{*{20}c}{a_1}&{a_2}&{a_3}&{a_1}&{a_2}\\{b_1}&{b_2}&{b_3}&{b_1}&{b_2}\\{c_1}&{c_2}&{c_3}&{c_1}&{c_2}\\\end{array}}\right)$ Tot slot teken (of denk) je 6 pijltjes zoals aangegeven:
Dus: determinant= a1b2c3 + a2b3c1 + a3b1c2 - a3b2c1 - a1b3c2 - a2b1c3
|