|
Voorbeeld
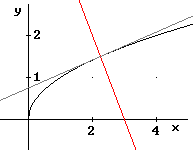
Bereken in graden nauwkeurig de hoek waaronder de grafieken van $f(x)=\sqrt{x}$ en $g(x)=-2x+6$ elkaar snijden.
Uitwerking
Bereken eerst het snijpunt:
$\sqrt{x}=-2x+6$
$x=(-2x+6)^2$
$x=4x^2-24x+36$
$4x^2-25x+36=0$
$4x^2-9x-16x+36=0$
$x(4x-9)-4(4x-9)=0$
$(x-4)(4x-9)=0$
$x=4$ (v.n.) of $x=2\frac{1}{4}$
$f$ en $g$ snijden in $x=2\frac{1}{4}$
|
Vervolg...
$\eqalign{f'(x)=\frac{1}{2\sqrt{x}}}$
$f'(2\frac{1}{4})=\frac{1}{3}$
$\tan\alpha=\frac{1}{3}$
$\alpha\approx18,4^\circ$
$\tan{\alpha}=-2$
$\beta\approx-64,4^\circ$
De gevraagde hoek is $\alpha-\beta\approx82^\circ$
|