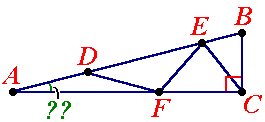Neem eerst een concreet voorbeeld. Bijvoorbeeld $\angle$A=20$^o$.

• $\angle$A=20$^o$
• $\angle$AFD=20$^o$
• $\angle$ADF=140$^o$
• $\angle$FED=40$^o$
• $\angle$DFE=100$^o$
• $\angle$EFC=60$^o$
• $\angle$FCE=60$^o$
• $\angle$ECB=30$^o$
• $\angle$B=75$^o$

Maar dat klopt niet want $\angle$A+$\angle$B=90$^o$

Neem $\angle$A=x$^o$.

• $\angle$A=x
• $\angle$AFD=x
• $\angle$ADF=180-2x
• $\angle$FED=2x
• $\angle$DFE=180-4x
• $\angle$EFC=3x
• $\angle$FCE=3x
• $\angle$ECB=90-3x
• $\angle$B=$\large\frac{3x+90}{2}$

Nu geldt:

$\angle$A+$\angle$B=90$^o$
x+$\large\frac{3x+90}{2}$=90$^o$
x=18$^o$

Controle:

• $\angle$A=18$^o$
• $\angle$AFD=18$^o$
• $\angle$ADF=144$^o$
• $\angle$FED=36$^o$
• $\angle$DFE=108$^o$
• $\angle$EFC=54$^o$
• $\angle$FCE=54$^o$
• $\angle$ECB=36$^o$
• $\angle$B=72$^o$

$\angle$A+$\angle$B=18$^o$+72$^o$=90$^o$. Klopt!