Centrum- en spreidingsmaten

Centrummaten:

• het rekenkundig gemiddelde
• de mediaan
• de modus

Spreidingsmaten:

• spreidingsbreedte
• kwartielafstand
• standaardafwijking

Zie verwerken van data

Steekproeven

Een steekproef is representatief als zij een juiste afspiegeling is van de gehele populatie.

Een representatieve steekproef zal in elk geval voldoende groot en aselect moeten zijn.

De populatieproportie $p$ van een populatie is het aantal elementen met een bepaald kenmerk in de populatie gedeeld door totaal aantal elementen in de populatie.

De steekproefproportie $\widehat p$ van een steekproef is het aantal elementen met een bepaald kenmerk in de steekproef gedeeld door het aantal elementen in de steekproef.

Aselect betekent dat elk element van de populatie dezelfde kans heeft om in de steekproef te worden opgenomen.

Opdracht 1

Hier zie je een steelbladdiagram met de proefwerkcijfers van 3B.

1. Bereken het gemiddelde en de standaardafwijking van de proefwerkcijfers op 1 decimaal nauwkeurig.
2. Bepaal de kwartielen en de mediaan en teken het boxplot.
3. Bereken de spreidingsbreedte en de kwartielafstand.
4. Wat is hier de modus?

Opdracht 2

Van de 1415 leerlingen van een school hebben 380 leerlingen een bijbaantje. Bij een onderzoek naar vrijetijdsbestedingen worden 65 leerlingen ondervraagd. Hiervan blijken 25 leerlingen een bijbaantje te hebben.

1. Is het waarschijnlijk dat hier sprake is van representatieve steekproef?
2. Hoeveel leerlingen met een bijbaantje zitten er in de steekproef van lengte 65 in het geval $\widehat p$ gelijk is aan $p$?

Opdracht 3

Leerlingen van schoolkrant vragen aan het begin van de kleine pauze aan de leerlingen bij de buitendeur wat ze vinden van het voorgenomen rookverbod op het terrein van school.

• Wat is er mis met deze manier van onderzoek?

Opdracht 1

1. $\mu$ = 4,4 en $\sigma$ = 1,2
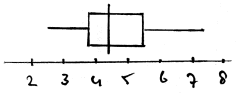
2. mediaan = 4,4
   $q_1$=3,75 en $q_3$=5,3
   
3. spreidingsbreedte = 7,2 $-$ 2,4 = 4,8
   kwartielafstand = 5,3 $-$ 3,75 = 1,55
4. modus=4,5

Opdracht 2

1. $p=\frac{380}{1415}\approx0,27$
   $\widehat p=\frac{25}{65}\approx0,38$
   $\widehat p$ wijkt erg ver af van $p$, dus het is niet waarschijnlijk dat hier sprake is van een representatieve steekproef.
2. Voor $a$ als aantal leerlingen met een bijbaantje in de steekproef zou moeten gelden dat $\frac{a}{65}=0,27$, dus $a\approx18$ moeten zijn.

Opdracht 3

De groep leerlingen die in de kleine pauze naar buiten gaat is geen goede afspiegeling van de schoolpopulatie. Sterker nog de kans dat een 'roker' in de steekproef wordt opgenomen is waarschijnlijk veel groter dan van een 'niet-roker'.