De normale verdeling

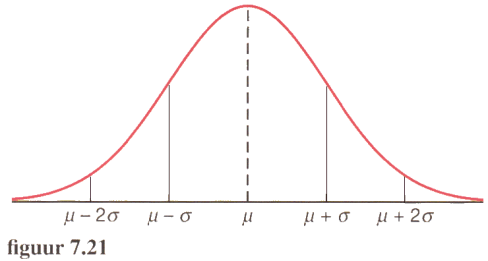
Een paar eigenschappen van een normale verdeling:

• klokvormig
• symmetrisch t.o.v. het gemiddelde.
• gemiddelde, mediaan en modus vallen samen
• de verdeling wordt bepaald door de verwachtingswaarde en de standaarddeviatie

Vuistregels bij de normale verdeling

1. 68% van de gegevens wijkt op z'n hoogst één keer de standaarddeviatie af van de verwachtingswaarde
2. 95% van wijkt op z'n hoogst twee keer de standaarddeviatie af van de verwachtingswaarde

Toepassen van de vuistregels

Gegeven is dat de lengte van mannen normaal verdeeld is met $\mu=178\,cm$ en $\sigma=8\,cm$. Je kunt dan (bijvoorbeeld) de volgende verdeling maken:

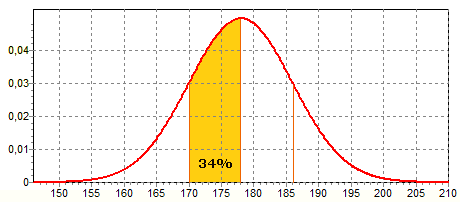
Dus 34% van de mannen heeft een lengte tussen 170 en 178 cm.

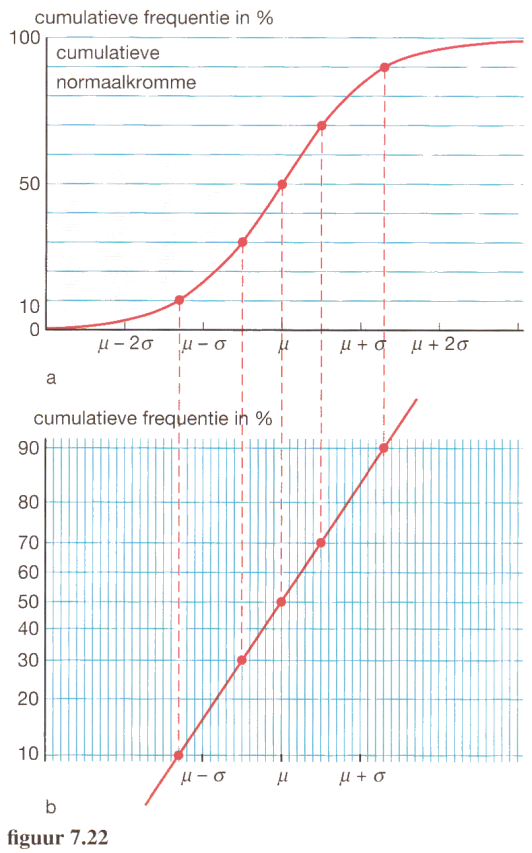
Normaal waarschijnlijkheidspapier

Bij een normale verdeling hoort een rechte lijn op normaal-waarschijnlijkheidspapier.

Je kunt $\mu$ aflezen bij de relatieve cumulatieve frequentie $50$. Je kunt $\mu + \sigma$ aflezen bij de relatieve cumulatieve frequentie $84$. Hieruit volgt $\sigma$.

Opdracht 1 (18)

Het gewicht van de mandarijnen uit een grote partij is normaal verdeeld met een gemiddelde van 80 gram. Verder is bekend dat 16% van de mandarijnen minder dan 76 gram weegt.

• Bereken de standaardafwijking

Opdracht 2 (A19)

Van 200 konijnen is het gewicht normaal verdeeld met een gemiddelde van 2,1 kg en een standaardafwijking van 0,3 kg.

1. Hoeveel procent van de konijnen is zwaarder dan 2,7 kg?
2. Hoeveel konijnen hebben een gewicht tussen 1,5 en 2,4 kg?
3. Hoeveel konijnen zijn er lichter dan 1,8 kg?
4. Wat weet je van de gewichten van de zwaarste konijnen in deze groep?

Opdracht 3 (A25)

Van een grote groep mannen is de lengte normaal verdeeld. Verder is bekend dat 15% korter is dan 1,70 m en 25% langer dan 1,85 m. Gebruik het normaal-waarschijnlijkheidspapier om uit te zoeken hoe groot het gemiddelde en de standaarddeviatie van de lengte zijn. Rond af op gehele centimeters.

• normaal-waarschijnlijkheidspapier

Opdracht 4 (A26)

Een bioloog onderzoekt van enkele soorten planten de lengte van de bladeren. Van elke soort zet hij de resultaten in mm uit op normaal-waarschijnlijkheidspapier. Telkens blijkt de lengte normaal verdeeld te zijn.

1. De lijnen van de soorten $A$ en $B$ zijn evenwijdig. Wat weet je van de bladlengte van de soorten $A$ en $B$?
2. De lijn bij soort $A$ is steiler dan die hoort bij soort $C$. Wat volgt hieruit?
3. De lijnen bij de soorten $C$ en $D$ snijden elkaar is het punt (48,80). Wat kan je zeggen van de soorten $C$ en $D$?
4. De gemiddelde bladlengte van soort $B$ is gelijk aan die van soort $D$. Wat weet je van de lijnen bij de soorten $B$ en $D$ op normaal-waarschijnlijkheidspapier?

Opdracht 1

16% weegt minder dan 76 gram, dus 76 ligt één standaardafwijking van het gemiddelde af. De standaardafwijking is 80-76=4 gram.

Opdracht 2

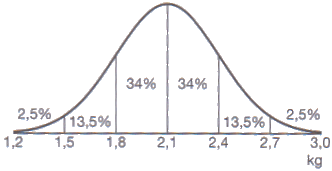
1. 2,5%
2. 13,5% + 68% = 81,5%. 0,815·200=163 konijnen
3. 2,5% + 13,5% = 16%, dus 0,16·200=32 konijnen
4. $\frac{5}{200}$·100%=2,5%, dus deze hebben een gewicht van meer dan 2,7 kg.

Opdracht 3

Bij 170 cm hoort 15%.
Bij 185 cm hoort 75%.
Lees af bij 50% dat $\mu=179\,cm$.
Lees af bij 84% dat $\mu+\sigma=188$, dus $\sigma=188-179=9\,cm$

• normaal-waarschijnlijksheidspapier

Opdracht 4

1. Evenwijdig betekent dezelfde standaardafwijking
2. Dat de bladlengte van soort A een kleinere standaardafwijking heeft dan die van soort C.
3. Dat zowel bij soort C als bij soort D 80% van de bladeren korter is dan 45 cm.
4. De lijnen bij B en D moeten elkaar dan snijden op een hoogte van 50.