|
Gemiddelde en standaardafwijking van een proportie
Bij een steekproevenverdeling is de steekproefproportie $\widehat p$ bij een voldoende grote steekproef $n$ bij benadering normaal verdeeld.
Hierbij is het gemiddelde $\mu$ gelijk aan de populatieproportie.
Voor de standaardafwijking $\sigma$ geldt:
$\eqalign{\sigma=\sqrt{\frac{\widehat p(1-\widehat p)}{n}}}$
Voorbeeld 1
Men neemt 800 steekproeven van lengte 250 bij een populatieproportie van 0,350. Hieruit volgt dat de bijbehorende standaardafwijking gelijk is aan 0,030.
$n=250$ en $\widehat p=p=0,350$ geeft:
$\eqalign{\sigma=\sqrt{\frac{0,350\cdot0,650}{250}}}=0,0301...\approx0,030$
Berekening van de steekproefomvang
Je kunt bij een gegeven betrouwbaarheidsinterval de steekproefomvang berekenen.
Aanpak
-
Bepaal $\widehat p$ en $\sigma$
-
Stel met de formule een vergelijking op
-
Los de vergelijking op met je GR.
|
Steekproef en betrouwbaarheidsinterval
Het 95%-betrouwbaarheidsinterval geeft aan dat bij het steeds nemen van een nieuwe aselecte steekproef uit dezelfde populatie 95% van de daarbij opgestelde intervallen de populatieproportie bevat.
Het 95%-betrouwbaarheidsinterval is:
-
$[\widehat p-2\sigma,\widehat p+2\sigma]$
Hierin is $\widehat p$ de steekproefproportie en $\sigma$ de standaardafwijking.
Het 68%-betrouwbaarheidsinterval is:
-
$[\widehat p-\sigma,\widehat p+\sigma]$
Voorbeeld 2
Twee dagen voor de verkiezingen voor de Tweede Kamer wordt aan 1200 stemgerechtigde Nederlanders gevraagd of ze van plan zijn te gaan stemmen. Van deze 1200 zeggen 756 inderdaad te gaan stemmen
-
Bereken het 95%-betrouwbaarheidsinterval van de stemgerechtigde Nederlanders die van plan zijn te gaan stemmen.
Uitgewerkt
$\eqalign{\widehat p=\frac{756}{1200}\approx0,63}$ en $\eqalign{\sigma=\sqrt{\frac{0,63\cdot0,37}{1200}}\approx0,013937...}$
Het 95%-betrouwbaarheidsinterval is $[0,602;0,658]$
|
|
Voorbeeld 3
Bij een onderzoek vindt men een 95%-betrouwbaarheidsinterval van [0,555;0,605].
-
Bereken de steekproefomvang
Uitwerking
Het interval $[0,555;0,605]$ staat voor $[\mu-2\sigma;\mu+2\sigma]$, dus tussen 0,555 en 0,605 zit $4\sigma$ verschil. Dus geldt:
-
$4\sigma=0,605-0,555=0,05$ dus $\sigma=0,0125$.
$\mu$ ligt in het midden van 0,555 en 0,605, dus geldt:
-
$\eqalign{\mu=\frac{0,555+0,605}{2}=0,58}$
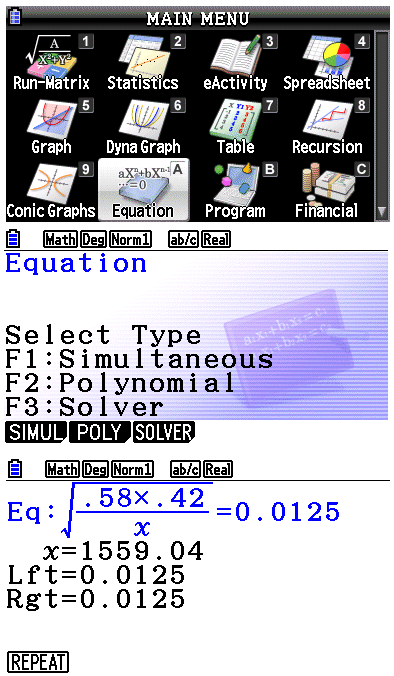
Vul nu de formule $\eqalign{\sigma=\sqrt{\frac{\widehat p(1-\widehat p)}{n}}}$ in:
-
$\eqalign{\sigma=\sqrt{\frac{0,58\cdot0,42}{n}}=0,0125}$
Met je GR kan je dan de vergelijking oplossen.
|
|
|
Opdracht 1 (A30)
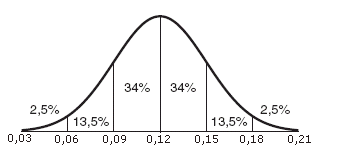
Een fabrikant van wasmiddelen neemt een jaar (365 dagen) lang elke dag een steekproef van 117 pakken. Hieruit blijkt dat 12,0% van de pakken te weinig wasmiddel bevat.
Het percentage pakken in een dagproductie met te weinig wasmiddel is normaal verdeeld met een standaardafwijking van 3,0%.
-
Toon aan dat dit percentage van 3,0% juist is.
-
Bij hoeveel van de steekproeven verwacht je dat er minstens 18 pakken zijn met te weinig inhoud?
-
Hoeveel dagen van dat jaar bevatten naar verwachting 7 of minder pakken in de steekproef te weinig wasmiddel?
-
De bedrijfsleider beweert dat het vaak genoeg voorkomt dat in een steekproef hoogstens 2 pakken zitten met te weinig inhoud. Kan dit kloppen? Leg uit.
Denk aan de vuistregels van de normale verdeling!
|
Opdracht 2 (A35)
Bij de presidentsverkiezing in een land moet gekozen worden tussen de kandidaten A en B. In een peiling die voorafgaat aan de verkiezingen zeggen 935 mensen te gaan stemmen. Hiervan zeggen 487 op kandidaat A te gaan stemmen, de anderen kiezen voor kandidaat B.
-
Onderzoek of je met een betrouwbaarheid van 95% kunt zeggen dat kandidaat A de verkiezingen zal gaan winnen.
Opdracht 3 (A39)
Bij een onderzoek onder D66-stemmers blijkt dat 55% het koningshuis wil behouden. Het bijbehorende betrouwbaarheidsinterval was $[0,49;0,61]$.
-
Hoeveel D66-stemmers zijn ondervraagd als het een 95%-betrouwbaarheidsinterval betreft?
|
|
Opdracht 1
-
n=117 en $\widehat p=p=0,120$ geeft:
$\eqalign{\sigma=\sqrt{\frac{0,120\cdot0,880}{117}}\approx0,0300...}$
Het percentage van 3,0% is juist.
-
Zie boven. $\eqalign{\frac{18}{117}\approx0,1538...}$. Er zit 13,5%+2,5%=16% boven 0,15, Dat is dan op 0,16·365=58 dagen.
-
Zie boven. $\eqalign{\frac{7}{117}\approx0,0598...}$. Er zit 2,5% onder 0,06. Dat is dan op 0,025·365=9 dagen.
-
Zie boven. $\eqalign{\frac{2}{117}\approx0,0170...}$. Dat is zelfs kleiner dan 0,03 dus erg waarschijnlijk is het niet. De bedrijfsleider kletst maar wat...:-)
|
Opdracht 2
De steekproefproportie van de mensen die zeggen op A te gaan stemmen is $\eqalign{\widehat p=\frac{487}{935}=0,5208...}$.
De bijbehorende standaarddeviatie is:
$\eqalign{\sigma=\sqrt{\frac{0,5208...\cdot0,4791...}{935}}=0,0163...}$
Het 95%-betrouwbaarheidsinterval wordt dan:
$[\widehat p-2\sigma;\widehat p+2\sigma]$
$[0,488...;0,553...]$
Om de verkiezingen te winnen moet kandidaat A 50% van de stemmen krijgen. Dus $p\gt0,5$, maar omdat $0,488$ kleiner is dan $0,5$ kun je dat nu niet met 95%-zekerheid zeggen.

|
|
Opdracht 3
Bij een 95%-betrouwbaarheidsinterval weet je dat $4\sigma=0,61-0,49=0,12$. Dus $\sigma=0,03$.
$\eqalign{\widehat p=\frac{0,49+0,61}{2}=0,55}$
Vul de formule $\eqalign{\sigma=\sqrt{\frac{\widehat p(1-\widehat p)}{n}}}$ in:
$\eqalign{\sqrt{\frac{0,55\cdot0,45}{n}}=0,03}$
Deze vergelijking kan je oplossen met je GR...
Er zijn 275 D66-stemmers ondervraagd.
|

Zie F3: Solver
|
|