|
Convergeren en divergeren
De webgrafiek van de differentievergelijking $u_n=a\cdot u_{n-1}+b$ heeft te maken met de lijnen $y=ax+b$ en $y=x$. De x-coördinaat het snijpunt van deze lijnen heet het dekpunt van de differentievergelijking.
Je berekent het denkpunt $\overline u$ door de vergelijking $\overline u=a\cdot\overline u+b$ op te lossen.
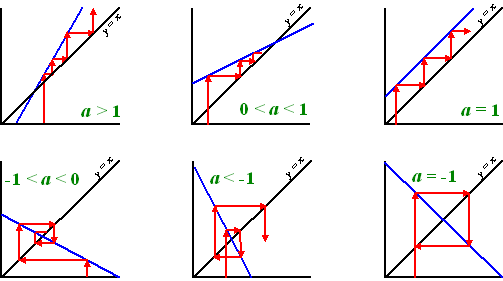
©hhofstede.nl
Voor $a\lt-1$ of $a\gt1$ is de rij divergerend.
Voor $-1\lt a\lt1$ is de rij convergerend.
Voor $a=-1$ of $a=1$ is de rij alternerend.
-
Zie ook blz 168 in je boek
|
Een directe formule
De directe formule van $u_n=a\cdot u_{n-1}+b$ is:
-
$u_n=A\cdot a^n+\overline u$
Waarij $\overline u$ het dekpunt is en $A$ een constante.
Aanpak
-
Bereken het dekpunt
-
Gebruik de startwaarde om $A$ te berekenen.
Voorbeeld
Je zet €10.000 op een spaarrekening. Vervolgens zet je elke maand €100 op de spaarrekening. Over het tegoed krijg je 0,5% rente per maand.
-
Wat is je spaartegoed na 12 jaar?
-
Na hoeveel maanden is je tegoed voor het eerst groter dan €60.000?
Zie uitwerking
|