|
De stelling van Pythagoras
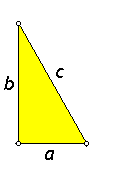 In de rechthoekige driehoek ABC zijn de zijden $a$ en $b$ de rechthoekszijden. De zijde $c$ noemen we de schuine zijde of hypotenusa. In de rechthoekige driehoek ABC zijn de zijden $a$ en $b$ de rechthoekszijden. De zijde $c$ noemen we de schuine zijde of hypotenusa.
De stelling van pythagoras luidt:
"In een rechthoekige driehoek is het kwadraat van de hypotenusa gelijk aan de som van de kwadraten van de rechthoekszijden."
Anders geformuleerd: $a^2+b^2=c^2$
|