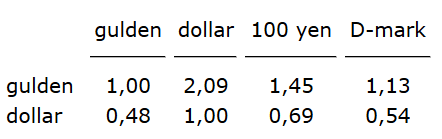|
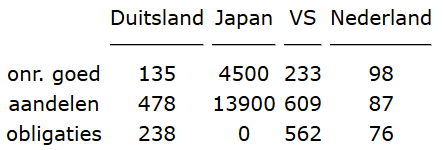
Opgave Een beleggingsfonds belegt in onroerend goed, aandelen en obligaties. Het fonds doet de beleggingen in Duitsland, Japan, de VS en Nederland. Hieronder staat een overzicht van de beleggingen, uitgedrukt in de munteenheid van de betreffende landen. Alle getallen moeten met 1 miljoen vermenigvuldigd worden.
Het fonds wil de aandeelhouder een overzicht presenteren van de beleggingen. Omdat de meeste aandeelhouders in Nederland wonen, maakt het fonds een overzicht in guldens. Daarnaast maakt ze voor haar buitenlandse aandeelhouders een overzicht in dollars. Bij de berekeningen gaat het fonds uit van de volgende koersen.
In de tabel kun je bijvoorbeeld aflezen dat 1 dollar f 2,09 waard is.
Uitwerking a. De matrix $B$: $\begin{array}{*{20}c}B&{\begin{array}{*{20}c}D&{Japan}&{VS}&{NL}\\\end{array}}\\{\begin{array}{*{20}c}{onr.goed}\\{aandelen}\\{obligaties}\\\end{array}}&{\left({\begin{array}{*{20}c}{135}&{4500}&{233}&{98}\\{478}&{13900}&{609}&{87}\\{238}&0&{562}&{76}\\\end{array}}\right)}\\\end{array}$ Op grond van het bovenstaande weten we in ieder geval dat K een matrix moet worden met 4 rijen. Omdat we de beleggingen zowel in gulden als in dollars willen uitrekenen zal deze matrix 2 kolommen moeten hebben. b. De matrix $K$: $\begin{array}{*{20}c}K&{\begin{array}{*{20}c}{gulden}&{dollar}\\\end{array}}\\{\begin{array}{*{20}c}{gulden}\\{dollar}\\{100yen}\\{D-mark}\\\end{array}}&{\left({\begin{array}{*{20}c}{1,00}&{0,48}\\{2,09}&{1,00}\\{1,45}&{0,69}\\{1,13}&{0,54}\\\end{array}}\right)}\\\end{array}$ Je krijgt dan: $B\times K=\left({\begin{array}{*{20}c}{135}&{4500}&{233}&{98}\\{478}&{13900}&{609}&{87}\\{238}&0&{562}&{76}\\\end{array}}\right)\times\left({\begin{array}{*{20}c}{1,00}&{0,48}\\{2,09}&{1,00}\\{1,45}&{0,69}\\{1,13}&{0,54}\\\end{array}}\right)$ Zodat: $B\times K=\left({\begin{array}{*{20}c}{9989}&{4778}\\{30520}&{14597}\\{1139}&{543}\\\end{array}}\right)$ c. Dit is een overzicht van de beleggingen per soort in gulden en in dollar.
|