|
De zijde×hoogte-methode
Voor driehoeken geldt:
-
ene zijde × bijbehorende hoogte = andere zijde × de bijbehorende hoogte
Je kunt daarmee soms handig de onbekende lengtes in een driehoek uitrekenen.
Opgave 1
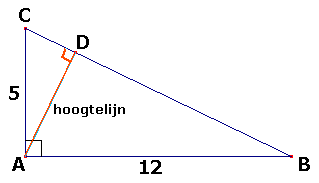
Gegeven is een rechthoekige $\Delta ABC$ met $\angle A=90^\circ$, $AB=12$ en $AC=5$. $AD$ is de hoogtelijn door het punt $A$.
-
Bereken exact de lengte van AD.
Uitgewerkt
Je kunt de oppervlakte van $\Delta ABC$ op twee manieren berekenen. Er geldt:
$\frac{1}{2}·AB·AC=\frac{1}{2}·BC·AD$
Invullen van de gegevens geeft:
$\frac{1}{2}·12·5=\frac{1}{2}·13·AD$
$60=13·AD$
$AD=4\frac{8}{13}$
Opgelost...:-)
|
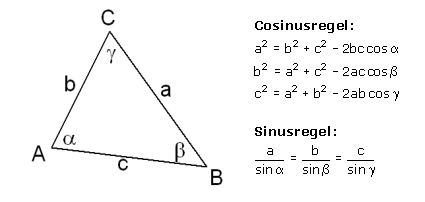
De sinusregel en de cosinusregel
In een willekeurige driehoek ABC geldt:
Opgave 2
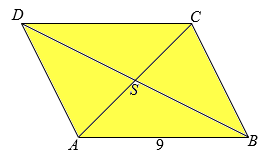
Van het parallellogram ABCD in de figuur is AB=9. AC=8 en BD=14.
-
Bereken de exacte waarde van AD.
Uitgewerkt
In $\Delta ABS$ geldt:
$\eqalign{
& A{S^2} = A{B^2} + B{S^2} - 2 \cdot AB \cdot BS \cdot \cos \angle ABS \cr
& {4^2} = {9^2} + {7^2} - 2 \cdot 9 \cdot 7 \cdot \cos \angle ABS \cr
& \cos \angle ABS = \frac{{19}}{{21}} \cr} $
In $\Delta ABD$ geldt:
$\eqalign{
& A{D^2} = A{B^2} + B{D^2} - 2 \cdot AB \cdot BD \cdot \cos \angle ABS \cr
& A{D^2} = {9^2} + {14^2} - 2 \cdot 9 \cdot 14 \cdot \frac{{19}}{{21}} \cr
& A{D^2} = 49 \cr
& AD = 7 \cr} $
|