|
Voorbeeld 2a
Stel een vergelijking op van de cirkel $c_1$ met middelpunt $M(3,-2)$ die de lijn $k:x+3y=7$ raakt.
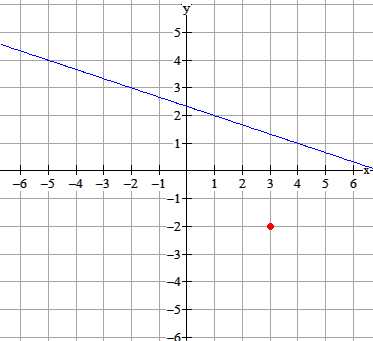
|
Uitwerking
De vergelijking voor $c_1$:
$(x-3)^2+(y+2)^2=r^2$ met $r=d(M,k)$
Neem lijn $m$ door $M$ en loodrecht op $k$.
Dat geeft: $m:3x-y=11$
Snijdt nu $m$ met $k$. Je krijgt dan het snijpunt $A(4,1)$.
Je kunt nu de straal van $c_1$ bepalen:
$\eqalign{
† & r = d(M,k) = d(M,A) = \sqrt {10}†† \cr
† & {c_1}:{(x - 3)^2} + {\left( {y + 2} \right)^2} = 10 \cr} $
|
|
Voorbeeld 2b
Stel een vergelijking op van de lijn $l$ die de cirkel $c_2:(x+2)^2+(y+1)^2=17$ raakt in het punt $B(2,0)$.
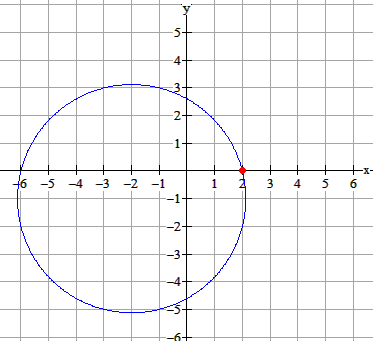
|
Uitwerking
Lijn $n$ gaat door het middelpunt $M(-2.-1)$ en $B(2,0)$.
$\eqalign{rc_n=\frac{0--1}{2--2}=\frac{1}{4}}$
De richtingscoŽfficiŽnt van $l$ is $rc_l=-4$
Invullen van $B(2,0)$ in $y=-4x+b$ geeft $b=8$
Dus: $l:y=-4x+8$
|
|
Voorbeeld 2c
Gegeven is de cirkel $c_3:x^2+y^2-2x-4y=0$. Bereken voor welke waarden van $b$ de lijn $y=2x+b$ de cirkel raakt.
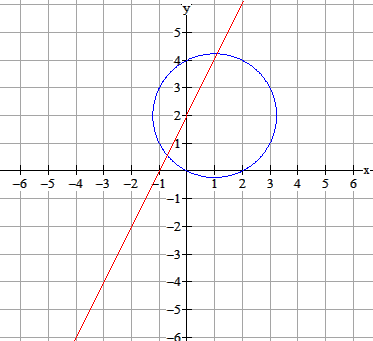
|
Uitwerking
$\begin{array}{l}
\left\{ \begin{array}{l}
{x^2} + {y^2} - 2x - 4y = 0\\
y = 2x + b
\end{array} \right.\\
{x^2} + {\left( {2x + b} \right)^2} - 2x - 4\left( {2x + b} \right) = 0\\
{x^2} + 4{x^2} + 4bx + {b^2} - 2x - 8x - 4b = 0\\
5{x^2} + 4bx - 10x + {b^2} - 4b = 0\\
5{x^2} + \left( {4b - 10} \right)x + {b^2} - 4b = 0\\
D = {\left( {4b - 10} \right)^2} - 4 \cdot 5 \cdot \left( {{b^2} - 4b} \right)\\
D = 16{b^2} - 80b + 100 - 20{b^2} + 80b\\
D =† - 4{b^2} + 100
\end{array}$
Omdat de lijn raakt aan de cirkel moet de discriminant nul zijn:
$\begin{array}{l}
†- 4{b^2} + 100 = 0\\
{b^2} - 25 = 0\\
{b^2} = 25\\
b =† - 5 \vee b = 5
\end{array}$
|