De eenheidscirkel

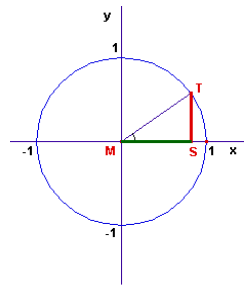
figuur 1

In figuur 1 zie je de eenheidscirkel. Het is een cirkel met een straal van 1. De ‘hoek’ is de hoek tussen het lijnstuk MT en het positieve deel van de x-as. Omdat de straal 1 is is de lengte van het 'rode lijnstuk' (verticaal) de sinus van de hoek en de lengte van het 'groene lijnstuk' (horizontaal) de cosinus van de hoek.

• Start het PHET-applet en beantwoord de volgende vragen.
  Zie eventueel https://www.wiskundeleraar.nl en dan hulpmiddelen voor de hyperlink.

Vraag 1

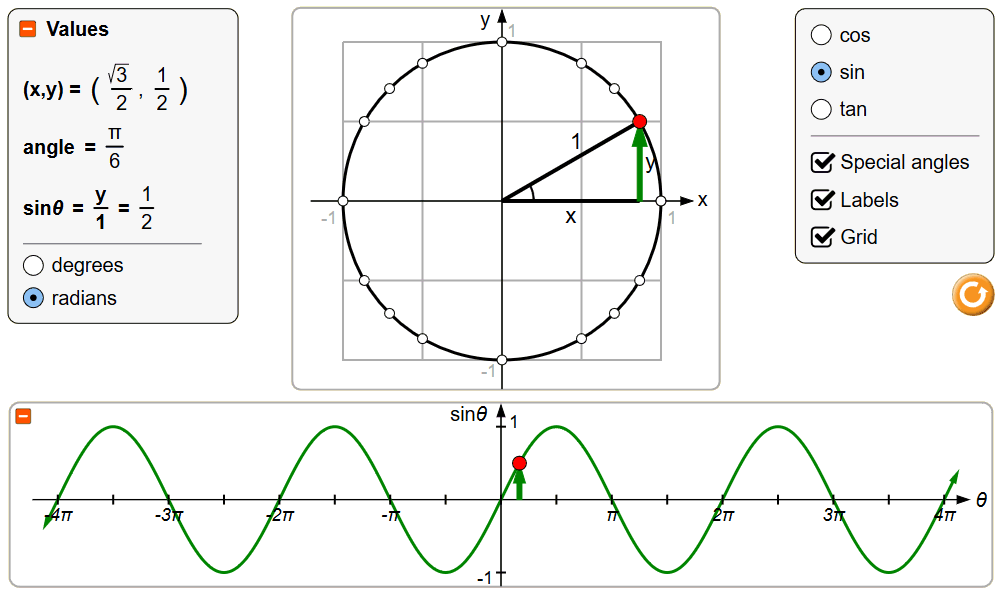
figuur 2

Stel het applet in als in figuur 2 aangegeven. Gebruik het applet bij de beantwoording van de vragen.

1. Hoe groot is de hoek in figuur 2 in graden?
2. Er zijn meer hoeken waarbij $\sin(\theta)=\frac{1}{2}$. Noem er 's een paar.
3. Wat is de sinus van een hoek van $8\frac{5}{6}\pi$?
4. Wat is de cosinus van een hoek van $1\frac{3}{4}\pi$? Wat is de cosinus van $-\frac{1}{4}\pi$? Zijn dat dezelfde hoeken?
5. Denk je dat het klopt als je zegt dat als twee hoeken dezelfde sinus hebben dat de hoeken dan ook gelijk zijn?

Vraag 2

Je kunt met je GR bij een gegeven hoek in radialen uitrekenen welke waarde van sinus of cosinus daarbij hoort.

1. Geef de sinus en de cosinus van een hoek van $\frac{2}{3}\pi$.
2. Welke hoek tussen $0$ en $\frac{1}{2}\pi$ geldt: $\sin(\alpha)=\frac{1}{2}\sqrt{2}$?
3. De sinus van $\frac{1}{3}\pi$ is gelijk aan de sinus van $\frac{2}{3}\pi$. De hoeken zijn samen $\pi$. Is dat toeval of geldt (in het algemeen) als $\alpha+\beta=\pi$ dan $\sin(\alpha)=\sin(\beta)$?
4. Ik heb twee hoeken $\alpha$ en $\beta$ en ik weet dat ze samen gelijk aan $\pi$ zijn. Wat weet je dan van de waarden van de sinus van $\alpha$ en $\beta$?
5. Zoiets als bij d. (maar dan anders) geldt ook voor de cosinus. Wat geldt er dan?

Vraag 3

Maar nu andersom.

1. Je weet dat $\sin(\alpha)=\frac{1}{2}\sqrt{3}$. Wat is dan $\alpha$?
2. Heb je bij a. wel ALLE mogelijke waarden voor $\alpha$ gegeven?
3. Je weet dat $\cos(\beta)=\frac{1}{2}\sqrt{3}$. Geef alle mogelijk waarden van $\beta$.

Bereken exact de waarde van $\alpha$ en geef ALLE mogelijke oplossingen.

1. $\cos(\alpha)=\frac{1}{2}$
2. $\sin(\alpha)=-\frac{1}{2}\sqrt{2}$
3. $\sin(\alpha)=0$
4. $\cos(\alpha)=1$
5. $\sin(\alpha)=-1$
6. $\sin(\alpha)=\cos(2\frac{1}{2}\pi)$