|
Lineaire of eerstegraadsfunctie
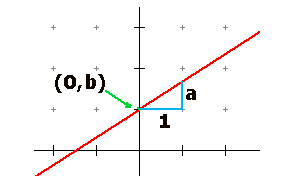 Voorkennis Voorkennis
-
Lineaire formules: grafieken tekenen
-
Formules opstellen: formule van een lijn opstellen, evenwijdige lijnen
-
Lineaire vergelijkingen: vergelijkingen oplossen, snijpunten van grafieken
-
Lineaire functies: origineel en beeld, notatie met haakje, f(x)=ax+b
-
Snijpunten: snijpunten met de x- of y-s, snijpunten van grafieken
Opgave 1
-
De lijn k gaat door de punten $(-2,1)$ en $(3,3)$. Geef een formule voor de lijn k.
-
Gegeven is de functie: $f(x) = 3x - 4$. Geef de coŲrdinaten van de snijpunten met de x- en y-as.
-
Gegeven zijn twee functies: $f(x) = -2x + 3$ en $g(x) = 3x - 1$. Bereken de coŲrdinaten van het snijpunt.
Formule van een lijn door twee punten
Als een lijn door $A$ en $B$ gaat dan kan je ook op deze manier een vergelijking van die lijn opstellen:
-
$\eqalign{a=\frac{y_B-y_A}{x_B-x_A}}$
-
$\eqalign{f(x)=a(x-x_A)+y_A}$
Voorbeeld
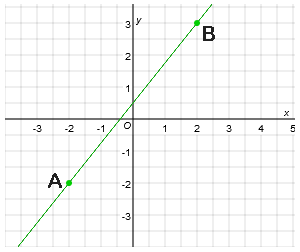
-
$\eqalign{a=\frac{3--2}{2--2}=\frac{5}{4}=1\frac{1}{4}}$
-
$\eqalign{f(x)=1\frac{1}{4}(x+2)-2}$
Toelichting
-
In de formule is $a$ de richtingscoŽfficient.
-
In de formule hebben we in het stuk na de richtingscoŽffiŽnt de coŲrdinaten van $A$ ingevuld. Dat moet niet, je had ook de coŲrdinaten van $B$ kunnen gebruiken:
$\eqalign{f(x)=a(x-x_B)+y_B}$
Opgave 2
-
Laat zien dat je bij bovenstaand voorbeeld dezelfde formule krijgt als je de coŲrdinaten van $B$ invult in het tweede deel van de formule.
Opgave 3
De lijn $k$ gaat door het punt $A(5,-2)$ en heeft als richtingscoŽfficiŽnt $a=-\frac{2}{3}$.
-
Leg uit dat $y=-\frac{2}{3}(x-5)-2$ een vergelijking is voor $k$.
Opdracht
Ga naar https://app.dwo.nl/vo/
-
login als gast
-
oude indeling
-
oefenmateriaal
-
formules, functies en grafieken
-
formules voor grafieken
-
functies raden lineair
-
functie bij rechte lijnen(2)
Gebruik daarbij de methode zoals deze hierboven staat beschreven.
-
Laat de haakjes staan! Normaal gesproken werk je natuurlijk de haakjes weg, maar vandaag hoeft dat niet.
|
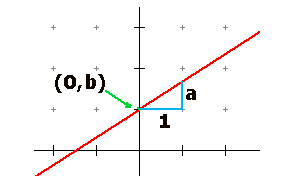 Voorkennis
Voorkennis