|
Kwadratische of tweedegraadsfunctie
De grafiek van de functie $y=a(x-p)^2+q$ is een parabool met het punt $(p,q)$ als top. We noemen dat de topformule. Je kunt daarmee snel zien wat de top is.
Opgave 4
Geef van coördinaten van de top van:
-
$y=2(x-4)^{2}+4$
-
$y=-(x+3)^{2}-11$
-
$y=-\frac{2}{3}(x+1\frac{1}{2})^{2}+2\frac{3}{4}$
-
$y=x^{2}+3$
-
$y=(x+7)^{2}$
Opgave 5
Start het online grafiekenprogramma op.
Je kunt een link vinden naar het programma op wiskundeleraar.nl bij de hulpmiddelen of type https://www.desmos.com/calculator in de adresbalk van je browser.
-
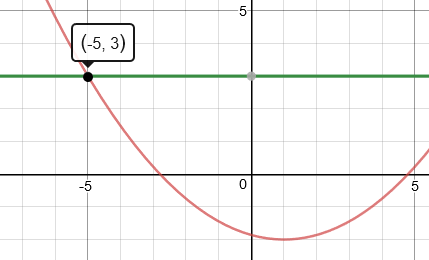
Als je in het grafiekenprogramma de functie $p:y=a(x-1)^2-2$ invult dan kan je met een schuifbalkje de waarde van $a$ veranderen.
-
Wat is de top van $p$?
-
Onderzoek de betekenis van $a$ voor de grafiek.
-
Wat is de (exacte) waarde van $a$ als de grafiek door het punt $(-5,3)$ gaat?
-
Neem $a=\frac{1}{5}$. Bepaal met het grafiekenprogramma voor welke waarde(n) van $x$ geldt: $y=3$?
Kan je dat ook berekenen? Wat moet je dan doen? Bereken de snijpunten van $p$ met de lijn $y=3$.
Translatie
|
Verticaal verschuiven
Je kunt de grafiek van een functie verticaal verschuiven door bij het functievoorschrift een getal op te tellen of af trekken.
Voorbeeld
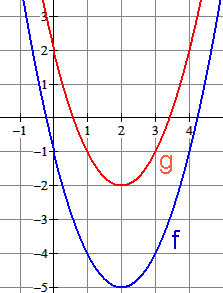
Gegeven is $f(x)=x^2-4x-1$. Als je nu 3 optelt bij $f$ dan krijg je $g(x)=x^2-4x+2$. In de tekening zie je dat je $f$ drie omhoog moet verschuiven om $g$ te krijgen.
|
Horizontaal verschuiven
Als je de grafiek van een functie naar links of rechts wilt verschuiven dan verander je in het functievoorschrift de variabele $x$ door $x-p$. De grafiek verschuift dan $p$ naar rechts.
Voorbeeld
Gegeven is $f(x)=x^2-4x-1$. Als je nu in het functievoorschrift van $f$ de variabele $x$ vervangt door $x+3$ dan schuift de grafiek 3 naar links.
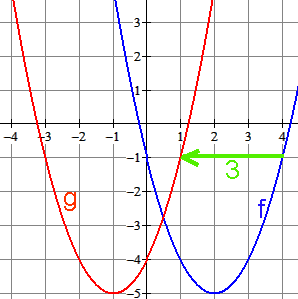
Je krijgt:
-
$g(x)=(x+3)^2-4(x+3)-1$
-
$g(x)=x^2+6x+9-4x-12-1$
-
$g(x)=x^2+2x-4$
|
Translatie over een vector
Je kunt een translatie (verschuiving) met een vector $(p, q)$ aangeven. Hierbij is $p$ de horizontale verplaatsing en $q$ de verticale verplaatsing.
Vraag 6
-
Ga met het grafiekenprogramma na dat als je de parabool $y=x^2$ transleert over de vector $(3, -1)$ je de functie $y=(x-3)^2-1$ krijgt.
Vraag 7
Gegeven is de parabool $p:y=x^2-4x+2$.
-
Over welke vector moet je transleren om de parabool $q:y=x^2+6x+5$ te krijgen?
-
Kan je dat ook berekenen?
Vraaag 8
Je transleert de parabool $p:y=-x^2+5x+5$ over de vector $(-2, 6)$. Je krijgt dan de parabool $g$.
-
Geef een mogelijk functievoorschrift van $g$. Schrijf je functievoorschrift in de vorm $y=ax^2+bx+c$.
| 

