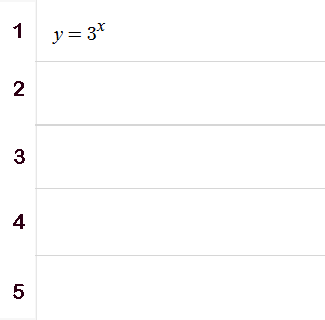|
Exponentiële functie
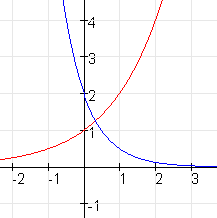
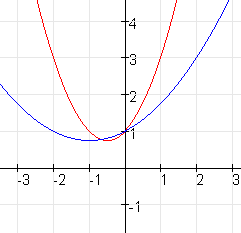
Opgave 13
Vermenigvuldigen t.o.v. de y-as
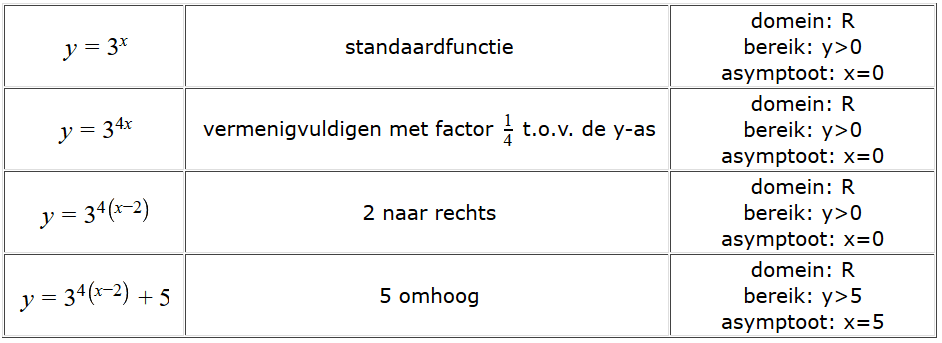
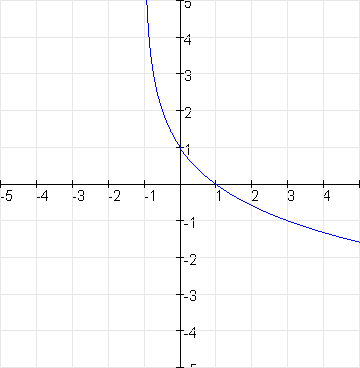
Voorbeeld 2 Geef het domein, bereik en eventuele asymptoten van:
Uitwerking
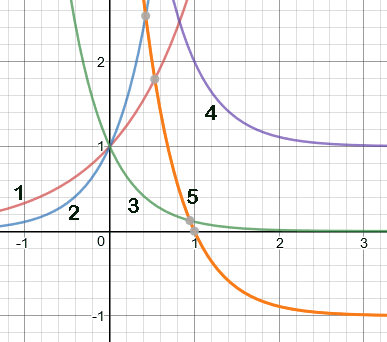
Opgave 14 Je ziet hier een schermafdruk uit het grafiekenprogramma. Het zijn een serie transformaties van $f(x)=3^x$. Links moeten de functievoorschriften staan van de grafieken aan de rechter kant.
Logaritmische functie
Opgave 15 Vul in:
Opgave 16 Gebruik de online rekenmachine of je grafische rekenmachine.
|