Voorbeeld 1

Gegeven: $
y=2\sqrt{x-4}+5
$

• Bepaal het domein en bereik

Aanpak:

• Het startpunt is $(4,5)$
• De grafiek gaat naar rechts
• De grafiek gaat omhoog

Conclusie:

• $D_f=[4,\to>$
• $B_f = [5, \to>$

Uitwerking

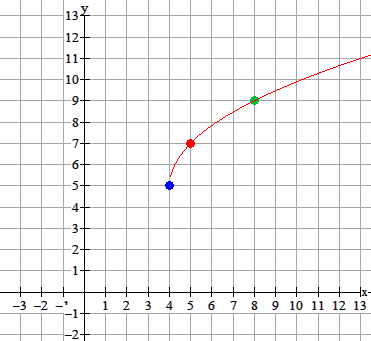
Het beginpunt is (4,5). Je kunt bedenken dat (5,7) een punt is van de grafiek. Het punt (8,9) is ook een punt van de grafiek...
Zie je dat?

Voorbeeld 2

Gegeven: $
y=2-3\sqrt{4-2x}
$

• Bepaal het domein en bereik

Aanpak

• Het startpunt is $(2,2)$
• De grafiek gaat naar links
• De grafiek gaat omlaag

Conclusie:

• $
  D_f=<\leftarrow,2]
  $
• $
  B_f = <\leftarrow ,2]
  $

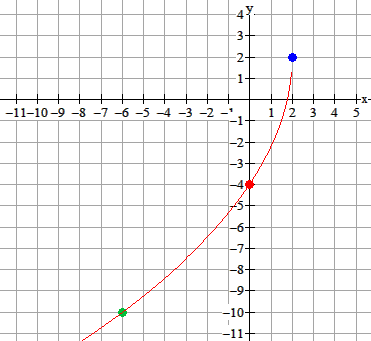
Uitwerking

Het beginpunt is (2,2). Het punt (0,-4) ligt op de grafiek. Wat dacht je van (-6,-10)?

Conclusie

In de praktijk komt het domein en bereik bepalen van een wortelfunctie neer op:

• Bepaal het startpunt.
• Loopt de grafiek naar links of naar rechts?
• Loopt de grafiek omhoog of omlaag?

Als je dat weet dan weet je hoe 't zit...

Opgave 21

Gegeven: $
f(x)=-2\sqrt{-x-1}+3
$.

• Bepaal het domein en het bereik.

Opgave 22

De grafieken $f(x)=\sqrt{x}$ en $g(x)=2\sqrt{x-3}$ snijden elkaar in $A$.

• Bereken de coördinaten van $A$.

Opgave 23

Los exact op:

1. $3x - 5\sqrt{x}-2=0$
2. $x - 4\sqrt x + 2 = 0$
3. $6x + \sqrt x = 7x - 20$

Opgave 24

Gegeven: $K=4+\sqrt{3p+1)}$

• Druk $p$ uit in $K$.