Vul $x=2$ in in de cirkelvergelijking. Je krijgt:
Schrijf de vergelijking voor de cirkel als:
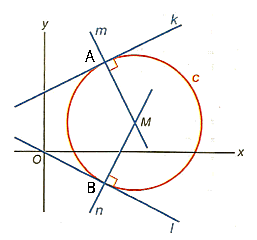
Het middelpunt van de cirkel is $M(3,1)$ en de straal is $\sqrt{5}$. De lijn $m$ door $A$ en $M$ heeft als richtingscoëfficiënt $rc_m=\frac{3-1}{2-3}=-2$. De raaklijn door $A$ aan de cirkel heeft als vergelijking:
De lijn $n$ door $B$ en $M$ heeft als richtingscoëfficiënt $rc_n=\frac{-1-1}{2-3}=2$. De raaklijn door $A$ aan de cirkel heeft als vergelijking:
|