Opgave
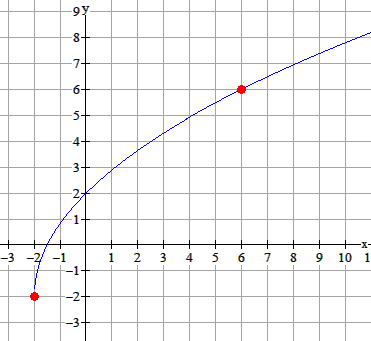
De wortelfunctie $f$ heeft als startpunt $(-2,-2)$ en gaat door het punt $(6,6)$.
-
Stel een functievoorschrift op voor de functie $f$.
Uitwerking
Ga uit van $f(x)=a+b\sqrt{c(x-d)}$.
Het startpunt is $(-2,-2)$, dus $a=-2$ en $d=-2$.
Het roosterpunt zit 8 eenheden boven het startpunt, dus $b=8$.
Het roosterpunt ligt 8 eenheden rechts van het startpunt, dus $\eqalign{\frac{1}{c}=8}$ zodat $\eqalign{c=\frac{1}{8}}$
Het functievoorschrift wordt: $f(x)=-2+8\sqrt{\frac{1}{8}(x+2)}$
Aangepast
Je kunt de breuk onder het wortelteken weg werken. Breng de factor $4$ onder het wortelteken. Je krijgt dan $
f(x) = - 2 + 2\sqrt {2\left( {x + 2} \right)}
$.
In de 'oude vorm' krijg je $
f(x) = - 2 + 2\sqrt {2x + 4}
$.
DeriveTM maakt er $
f(x) = 2\sqrt 2 \cdot \sqrt {x + 2} - 2
$ van. Ook leuk...
Toelichting
Voor de standaardvorm voor een wortelfunctie zou je dit voorschrift kunnen nemen:
Je kunt het functievoorschrift opvatten als een ketting van transformaties die je uitvoert op de standaard wortelfunctie $y=\sqrt{x}$.
Transformaties
$f(x)=\sqrt{x}$
-
vermenigvuldigen t.o.v. de y-as met de factor $
\eqalign{\frac{1}{c}}
$ geeft:
$f(x)=\sqrt{cx}$
-
horizontale verplaatsing over de vector $
\left( {\begin{array}{*{20}c}
d \\
0 \\
\end{array}} \right)
$ geeft:
$f(x)=\sqrt{c(x-d)}$
-
vermenigvuldigen t.o.v. de x-as met de factor $b$ geeft:
$f(x)=b\sqrt{c(x-d)}$
-
verticale verplaatsing over de vector $
\left( {\begin{array}{*{20}c}
0 \\
a \\
\end{array}} \right)
$ geeft:
$f(x)=a+b\sqrt{c(x-d)}$
Begrip en inzicht
Bij HAVO wiskunde B maken standaardfuncties en transformaties deel uit van het programma. Ik heb een leerroute gemaakt waarin leerlingen (naast die karakteristieke eigenschappen van standaardfuncties) leren hoe je grafieken kunt transformeren, hoe je daarbij formules kunt maken en hoe je aan een formule kan zien welke transformaties op de standaardfunctie zouden kunnen zijn toegepast.
|