|
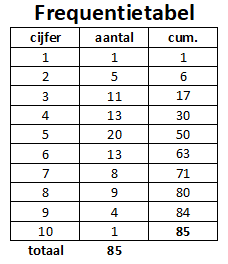
Vraag Gegeven een frequentietabel met 85 waarden.
Uitwerkingen De mediaan zit bij de 43e waarde. Dat is het cijfer 5. Je kunt dan $q_1$ vinden bij de 22e waarde. Dat is dan het cijfer 4. Net zo $q_3$ zit dan bij het 64e getal en dat is 7.
Toelichting Als je 85 waarden op volgorde zet van klein naar groot dan is de 43e waarde de mediaan. Nu is de vraag wat is nu de onderste helft en wat is nu de bovenste helft? Ik heb gekozen voor 1 t/m 43 voor de onderste helpt en voor 43 t/m 85 als bovenste helft. Ik had ook kunnen kiezen voor 1 t/m 42 en 44 t/m 85. Beide methode komen voor en het maakt doorgaans weinig verschil. Uitgewerkt Bij 1 t/m 42 ligt $q_1$ bij de 21e en 22e waarde. $q_1$ is dan 4. Bij 44 t/m 85 ligt $q_3$ bij het 64e en 65e getal. $q_3$ is dan gelijk aan 7.
In dit geval maakt het zelfs niets uit. Opmerkingen
Gevonden waarden
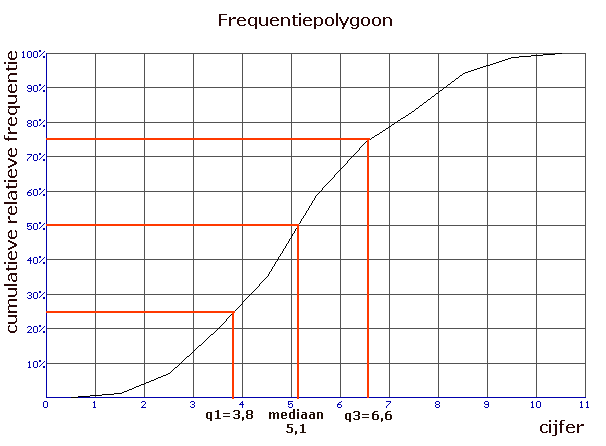
Somfrequentiepolygoon
Begrip en inzicht De kwartielafstand is een spreidingsmaat. Het is een handig tool om verdelingen te vergelijken. Het heeft weinig betekenis in absolute zin. Of je nu bij de onderste en bovenste helft de mediaan nu wel of niet mee moet tellen doet er weinig toe. Als je 't maar consequent toepast is er weinig aan de hand.
|